常见随机变量的概率分布及计算案例：二项分布、泊松分布

1.离散型随机变量常见分布

1）两点分布（0-1分布）

定义5 随机变量X只能取0或1，其概率分布为

则称X服从两点分布（p为参数）.

两点分布也称为0-1分布，其概率分布为

【例7】据统计，目前新生儿出生率中男女比例约为116：100，以X表示新生儿性别，则

求X的概率分布.

解　由题意知随机变量X服从0-1分布，其概率分布为

2）二项分布（X～B（n，p））

定义 6　若一个随机试验可以在相同的条件下重复进行n次，每次试验的结果互不影响，且一次试验只可能出现两种结果A或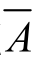，则在每次试验中，事件A出现的概率P（A）=p（0＜p＜1）都不变，且P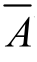（）=1-p.这种试验称为n重伯努利试验（简称伯努利试验）.

在n重伯努利试验中，事件A恰好发生k次的概率为

因为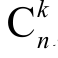pkqn-k恰好为二项式（p+q）n的展开式中的第k+1项，故我们称随机变量X服从参数为n，p的二项分布，记作X～B（n，p）.

特别地，当n=1时，二项分布即为两点分布.

【例 8】现有某种进口货物100件，每件货物可能为不合格品的概率是0.05，问100件货物中有2件不合格品的概率？

解　用X表示100件货物中的不合格品数，则X～B（n，p）.所以100件货物中有2件不合格品的概率为

3）泊松分布（X～P（λ））

定义7 如果随机变量X的概率函数为

则称X为服从参数为λ的泊松分布，记作X～P（λ），λ为参数.

当n充分大、p充分小时，可用λ=np（一般要求λ≤5）的泊松分布代替二项分布，即

【例 9】计算机硬件公司制造某种特殊型号的微型芯片，次品率达0.1%，记X为产品中的次品数，X～B（1000，0.001），各芯片成为次品相互独立，问在1 000只产品中至少有2只次品的概率？

解　由题意X～B（1000，0.001），其中n=1000，p=0.001，则可用λ=np =1000×0.001=1的泊松分布，即

代替二项分布.所以，1 000只产品中至少有2只次品的概率为

2.连续型随机变量常见分布

1）均匀分布（X～U（a，b））

定义8 如果随机变量X的概率密度为

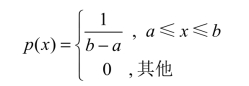
则称随机变量X服从在区间[a，b]上的均匀分布.(www.xing528.com)

若随机变量X服从在区间[a，b]上的均匀分布，则对于任意子区间[c，d]⊂[a，b]，有

上式说明X落在子区间[c，d]上的概率等于子区间长度与整个区间长度之比，而与子区间[c，d]在[a，b]中的位置无关.

【例 10】经过对某种内销产品的统计得知，其国内市场需求量最少是2 000单位，最多是5 000单位，而在2 000～5 000之间无任何明显的变化特征.现组织2 800单位的货源，求不能满足需求的概率.

解 设X为该种产品的国内市场需求量，依题意，X是[2000，5000]上的均匀分布，则有

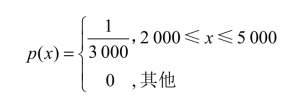
所以，不能满足需求的概率为

2）指数分布（X～E（λ））

定义9 若随机变量X的概率密度为

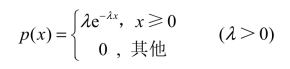
则称X服从参数为λ的指数分布，记作X～E（λ）.

【例 11】某品牌整流器的使用寿命X服从指数分布，其概率密度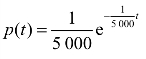（t＞0，单位：h）.问：

（1）整流器在1 000 h内失效的概率；

（2）使用寿命在1 000～2 000 h之间的概率；

（3）这种整流器使用2 000 h以上的概率.

3）正态分布（X～N（μ，σ2））

定义10 若连续型随机变量X的概率密度为

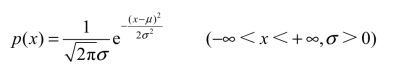
则称X服从参数为μ，σ的正态分布（或高斯分布），记作X～N（μ，σ2）.

对于X～N（μ，σ2）而言，p（x）在直角坐标系内的图形呈钟形，最大值点在x=μ处，如图3-9所示.曲线关于直线x=μ对称；在x=μ±σ处有拐点；当x→±∞时，曲线以x轴为渐近线；σ越大曲线越平缓，σ越小曲线越陡峭.对于X～N（0，1），最大值点在x=0处，如图3-10所示.

正态分布在概率统计的理论与应用中占有特别重要的地位，例如测量一批产品的长度或强度等质量指标所产生的误差，都可以看作或近似看作服从正态分布.

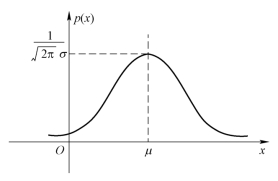
图3-9

图3-10

定义11 当μ=0，σ=1时，正态分布的概率密度称连续型随机变量X服从标准正态分布，记作X～N（0，1）.

标准正态分布的分布函数记为Φ（x），其概率密度记为φ（x），如图3-10所示.标准正态分布的概率计算公式如下：

一般正态分布的概率计算公式如下.

当X～N（μ，σ2）时，有

【例14】某公安系统通过公务员笔试考试拟录取前80名考生，实际参加考试的考生为2 000名，设考试成绩为X，且X～N（200，502），问录取分数线应定为多少分？

解　设录取分数线应定为a分，由题意有

查标准正态分布表（附表2）得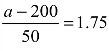，即a≈288.所以，录取分数线应定为288分.