【摘要】：所以，λ=12.若该城市发电厂每天供电量为80万kW·h，则任一天供电量不能满足需求的概率为
定义 3 对于随机变量X，若存在非负可积函数p（x）（-∞＜x ＜+∞），使得对任意实数a，b（a＜b），都有
则称X为连续型随机变量.其中，函数p（x）称为概率密度函数（简称概率密度），p（x）的图像称为概率密度曲线.
概率密度p（x）有以下性质：
（1）非负性，即p（x）≥0；
（2）完备性，即
根据定积分的几何意义可知，随机变量X落在区间（a，b）内的概率等于由直线x=a，x=b，曲线y=p（x）以及x轴围成的曲边梯形的面积，如图3-6所示；p（x）与x轴之间的面积为1，如图3-7所示.
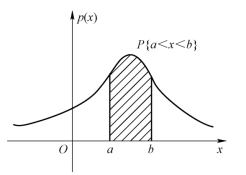
图3-6
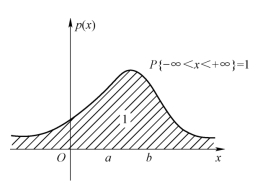
图3-7
注意：连续型随机变量X取任意值a的概率为0，即
(www.xing528.com)
【例3】设随机变量X的概率密度为
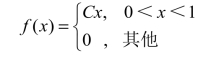
求：（1）系数C；（2）概率P（0.5≤X≤1）.
解 （1）由概率密度的完备性知
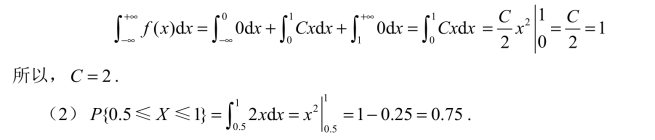
【例4】某城市每天耗电量不超过100万kW·h，该城市每天耗电率（即每天耗电量/100万kW·h）是一个连续型随机变量，它的概率密度为
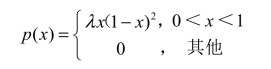
若该城市发电厂每天供电量为80万kW·h，则任一天供电量不能满足需求的概率为多少？
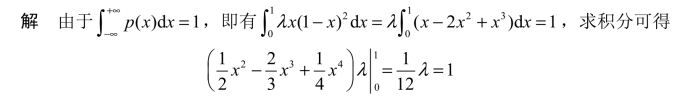
所以，λ=12.
若该城市发电厂每天供电量为80万kW·h，则任一天供电量不能满足需求的概率为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
