线性规划问题的图解法：解析和应用

图解法一般只能用来求解两个变量的线性规划问题，其直观简便，虽然应用范围较小，但有助于理解线性规划问题的几何意义和解的基本情况.

【例3】用图解法求解［例1］的线性规划问题

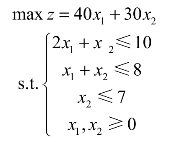
解 第一步，在平面直角坐标系x1Ox2中作直线

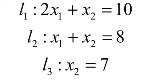
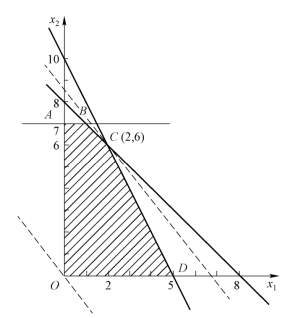
图2-1

如图2-1所示，阴影部分所有点（包括边界上的点）满足该问题的所有约束条件，则满足约束条件的所有点都是可行点，每一点代表该线性规划问题的一个可行方案，即一个可行解.所有可行点的集合称为该问题的可行域，图2-1中五边形OABCD内部及边界的阴影部分即为可行域，故该问题的可行解有无穷多个.

第二步，寻求最优解.

（1）将目标函数写成40x1+30x2=b （b为常数），选取b为不同值时，目标函数的图形是通过可行域的某一点或某些点的直线，该组直线互相平行，称为等值线.不妨令b=0，于是有，它是一条通过坐标原点的直线，称为0等值线.

（2）为寻求最优解，将通过原点的0等值线沿目标函数增大的右上方平移，到达顶点C时，z在可行域中取得最大值；如果继续向右上方平移，则等值线将离开可行域（即等值线与可行域没有交点），则点C（2，6）就是最优解，其最优值z=2×40+6×30=260.所以，最优解为x1=2，x2=6，最优值zmax=260.

【例 4】将［例3］中目标函数变为z=40x1+20x2，则以z为参数表示目标函数的直线组与约束条件2x1+x2≤10所示的可行域的边界平行.

(www.xing528.com)

图2-2

当z由小变大时最终将与线段CD重合（见图2-2），线段CD上任意一点都使z取得相同的最大值，此时线性规划问题有无穷多最优解.

这是线性规划问题无穷多最优解情况，当然，线性规划问题也可能无最优解的情况，这里就不做讨论了.

线性规划问题的解的情况可以归结为：

（1）唯一最优解；

（2）无穷多最优解（多重解）；

（3）无界解（有可行解但没有最优解）；

（4）无可行解.

上述结论对于两个以上变量的线性规划问题也是适用的.

习 题 2.5

某车间生产甲、乙两种产品，每件产品都要经过两道工序，即在设备A和B上加工，但两种产品的单位利润各不相同.已知生产单位产品所需的有效时间（单位：小时）即利润见表2-15，问生成甲、乙两种产品各多少件时，才能使所获利润最大？

表2-15