的经济效益分析产出分析与经济效益分析

1.分配方程组的解

由直接消耗系数定义，得

将其代入分配方程组①，得

则分配方程组③式可用矩阵形式表示为

这里A是直接消耗系数矩阵.

由矩阵④式可得

求解线性方程组⑤得到X.

2.投入方程组的解

将xij=aijxj 代入投入方程组②，得

由投入方程组⑥，得

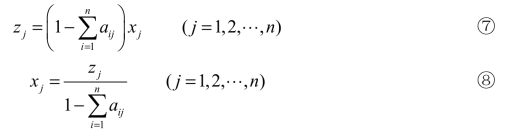
【例4】设某经济系统有三个部门，在某一生产周期内各部门间的直接消耗系数及最终产值如表2-10所示，求：

（1）各部门的总产出；

（2）各部门新创造的价值；

（3）部门间流量.

表2-10　单位：万元(www.xing528.com)

解 （1）设三个部门总产出x1，x2，x3组成矩阵为

直接消耗系数矩阵与最终产值矩阵分别为

其分配平衡方程组为

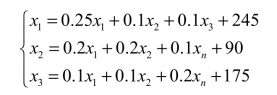
方程组的解为x1=400，x2=250，x3=300.

因此，三个部门在一个生产周期内的总产值分别为400万元、250万元、300万元.

（2）根据⑦式，得

因此，三个部门在一个生产周期内新创造的价值分别为180万元、150万元、180万元.

（3）由xij=aijxj 可算出部门间流量分别为

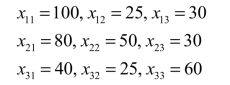
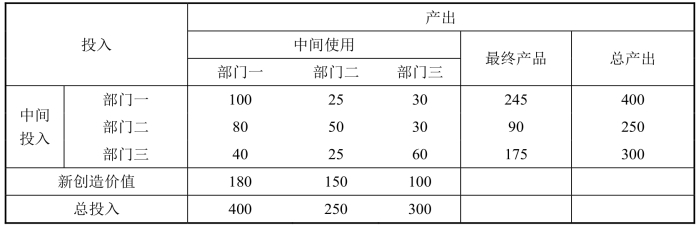
该经济系统的投入产出如表2-11所示.

表2-11　单位：万元

习 题 2.4

某经济系统有三个部门：煤矿、电力和铁路.在过去一年内，产业间流量和总产出如表2-12所示.求：（1）各部门最终产品的价值yi（i=1，2，3）；（2）各部门新创造的价值zj（j=1，2，3）；（3）直接消耗系数矩阵.

表2-12　单位：亿元