线性方程组的解及其条件

定理2　如果利用初等行变换将线性方程组AX=B的增广矩阵（AB）化为（CD），那么方程组AX=B与CX=D是同解方程组.

【例5】求［例2］中线性方程组的解.

解 对［例2］所得的行阶梯形矩阵进行初等行变换，得到行简化阶梯形矩阵为

所以，方程组的解为x1=1，x2=3，x3=2.

【例6】求［例3］中线性方程组的解.

解 对［例3］所得的行阶梯形矩阵进行初等行变换，得到行简化阶梯形矩阵为

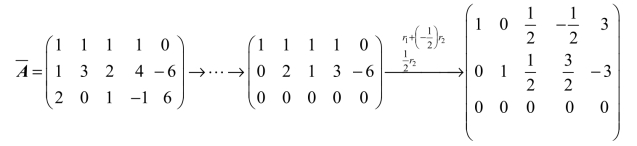
与原方程组同解的方程组为

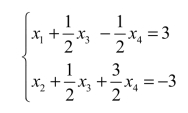
令x3=c1，x4=c2，得原方程组的解为

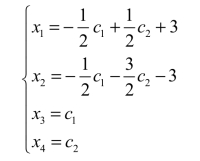
方程组中，c1，c2为任意常数.这种解的形式称为线性方程组的通解或一般解.

【例7】求解齐次线性方程组

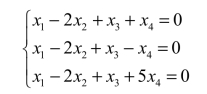
解　该齐次线性方程组的系数矩阵为

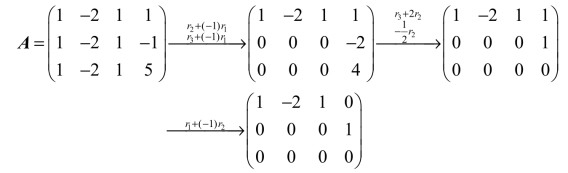
与原方程组同解的方程组为

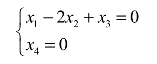
令x2=c1，x3=c2，得原方程组的通解为

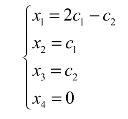
【例8】某百货商店出售四种型号的衬衫：小号、中号、大号和加大号.四种型号的衬衫售价分别为22元、24元、26元和30元.如果该商店某周共售出13件衬衫，销售收入为320元，并已知大号的销售量为小号和加大号的销售量总和，大号的销售收入也为小号和加大号销售收入的总和.问四种型号的衬衫各售出多少件？

解　设小号、中号、大号与加大号衬衫的销售量分别为x1、x2、x3、x4，由题意得

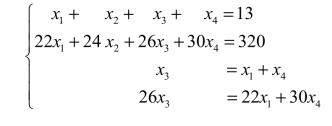
方程组变形为

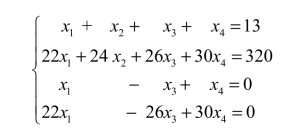
其增广矩阵化简得

(www.xing528.com)

所以，方程组的解为x1=1，x2=9，x3=2，x4=1，故小号、中号、大号和加大号衬衫的销售量分别为1件、9件、2件和1件.

【例 9】三家物流公司A1、A2、A3为运输需要，同意实行资源共享，由于运输工具与成本各异，他们达成了如下协议：

（1）每个公司总共工作10天（包括给自己家运输）；

（2）每个公司的日资金根据测算在30万～40万元；

（3）每个公司的日资金数应使每个公司的总收入与总支出相等.

表 2-5 是他们协商后制订出的工作天数的分配方案，请计算出他们每个公司应得的日资金.

表2-5

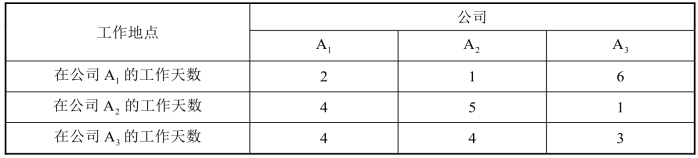
解　设x1表示公司A1的日资金，x2表示公司A2的日资金，x3表示公司A3的日资金.公司A1的10个工作日总收入为10x1，公司A1、公司A2和公司A3在公司A1的工作天数分别为2天、1天、6天，则公司A1的总支出为2x1+x2+6x3（万元）.由于公司A1总支出与总收入要相等，于是公司A1的收支平衡关系为2x1+x2+6x3=10x1.同理可得线性方程组为

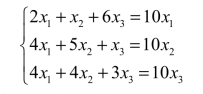
化简得三家公司的日资金数应满足的齐次线性方程组为

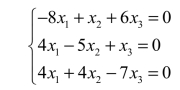
解齐次线性方程组，得它的通解为

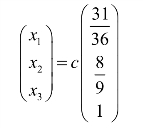
方程组中，c为任意实数.

由于每个公司的日资金为 30 万～40 万元，故选择c=36，则三家公司A1，A2，A3每天的日资金分别为31万元、32万元和36万元.

习 题 2.3

1.判断下列线性方程组解的情况.

2.当a、b为何值时，方程组

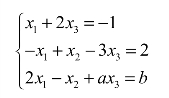
无解？有唯一解？有无穷多解？

3.当a取何值时，方程组

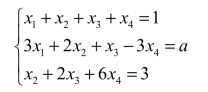
有解？并求出它的解.

4.求解下列线性方程组.

6.甲、乙、丙三位村民组成互助组，每人工作6天（包括为自己家干活的天数），刚好完成他们三家的农活，其中甲在甲、乙、丙三家干活的天数依次为2、2.5、1.5（天），乙在甲、乙、丙三家各干2天活，丙在甲、乙、丙三家干活的天数依次为1.5、2、2.5（天）.根据三人干活的种类、速度和时间，他们确定三人不必相互支付工资刚好公平.随后三人又合作到邻村帮忙干了2天（各人干活的种类和强度不变），共获得工资1 200元.请问他们应该怎样分配这1 200元工资才合理？