【摘要】:矩阵乘法定义 5 设矩阵A=(aij)m×s,B=(bij)s×n,称矩阵C=(cij)m×n 为矩阵A与B的乘积,记作注意:(1)只有当矩阵A的列数等于矩阵B的行数时,AB才有意义;(2)矩阵C=AB的行数等于矩阵A的行数m,列数等于矩阵B的列数n.注意:由于矩阵B有2列,矩阵A有3行,B的列数不等于A的行数,所以BA无意义.由[例5]可知,矩阵的乘法不满足交换律,即AB≠BA.即使矩阵A≠O,

矩阵乘法
定义 5 设矩阵A=(aij)m×s,B=(bij)s×n,称矩阵C=(cij)m×n 为矩阵A与B的乘积,记作

注意:(1)只有当矩阵A的列数等于矩阵B的行数时,AB才有意义;
(2)矩阵C=AB的行数等于矩阵A的行数m,列数等于矩阵B的列数n.
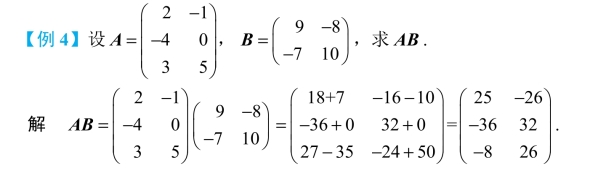
注意:由于矩阵B有2列,矩阵A有3行,B的列数不等于A的行数,所以BA无意义.
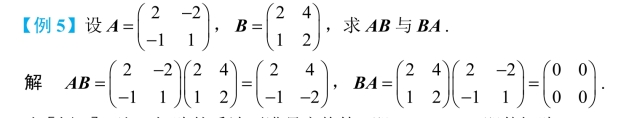
由[例5]可知,矩阵的乘法不满足交换律,即AB≠BA.即使矩阵A≠O,B≠O,也可能出现AB=O,即两个非零矩阵的乘积可能是零矩阵.也就是说AB=O,不一定有A=O或B=O.

由[例6]可知,矩阵乘法不满足消去律,即当AC=BC,且C≠O时,不一定有A=B,一般不能在等式两端都消去矩阵C.
矩阵乘法满足以下运算律:
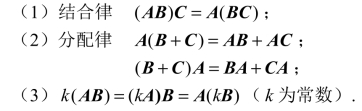
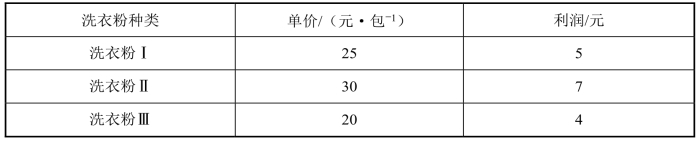
【例7】设有两家超市出售3种洗衣粉,某日销售量和每种洗衣粉的单价和利润分别见表2-2和表2-3.求两家超市出售洗衣粉的总收入和总利润.(https://www.xing528.com)
表2-2 单位:包

表2-3
解 两家超市某日出售洗衣粉的总收入和总利润如表2-4所示.
表2-4 单位:元

设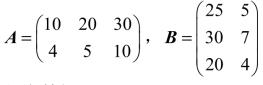 ,C=AB,C表示两家超市某日出售洗衣粉的总收入和总利润,即
,C=AB,C表示两家超市某日出售洗衣粉的总收入和总利润,即

习 题 2.1

3.计算下面的矩阵乘积.

4.已知 ,求AB与BA.
,求AB与BA.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




