题1 答案为E项。
观察题干发现,本题情况较多,因此,验证真假可采用“设特值”的方式。
注意题干的断定,只要某位陪审员认为证人在作案时间、作案地点或作案动机上“有一个做了伪证”,便属于题干所断定的“三分之二陪审员”之内,因此,不妨设陪审员共有9人,其中,2人认为证人在作案时间上做了伪证,2人认为证人在作案动机上做了伪证,2人认为证人在作案地点上做了伪证。在此情况下,完全符合题干断定,但与A、B、C和D项均不相符。
题2 答案为A项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
根据补充条件可知,惯犯可以作案多起,从而案件与作案者未必一一对应。因此,不妨设严重刑事案件共有10件,其中6件是同一人所为,且该罪犯就是已记录在案的350名惯犯之一,其余4件分别是其他4位人员所为,且这4位都吸毒。该情况满足题干的所有条件,但无法证明350名惯犯中有人吸毒,从而可以推出A项。B项与题干相违背,其余选项均与题干不符。
题3 答案为E项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
复选项Ⅰ,违反题干所给条件“两人历史成绩相同”,排除A项和D项。
复选项Ⅱ,若剩余那门成绩王平比李昌高出很多,则未必能得出所需结论。例如,剩余的一门成绩,王平是100分,李昌是60分;其他四门的平均成绩,王平是70分,李昌是71分。此时王平五门课程的平均成绩是高于李昌的,排除B项。
复选项Ⅲ,若王平其他课程分数比李昌高出很多,则未必能得出所需结论。例如,王平五门成绩分别为60、96、97、98、99,李昌五门成绩分别为60、61、62、63、100,此时王平五门课程的平均成绩是高于李昌的,排除C项。
题4 答案为D项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
A、B和E项,分别确定了成绩最高或最低的属性。但两者除金融市场外的四门课程,具体分数是多少、分差是多少均不知道,所以难以确定所需结论,排除A、B和E项。
C项,若剩余那门成绩杨玲比陈娜高出很多,则未必能得出所需结论。例如,剩余的那门成绩,杨玲是100分,陈娜是60分;其他三门的成绩,杨玲都是70分,陈娜都是71分。此时杨玲五门课程的平均成绩是高于陈娜的,排除C项。
D项表明,陈娜其余四门成绩均高于杨玲,因此可以得出所需结论。
题5 答案为B项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
对于张三的话,若三种球的数量分别是33、33和34只,则张三的话为假,故排除A、C和E项。对于李四的话,其反面为“每种球都少于34只”,若李四反面成立,则三种球数量之和最多为99只,不符合题干要求。因此李四的话为真,排除D项。
根据效用思维(已知答案,其余不看),可不用验证王五的话。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
对于王五的话,其反面为“至少有一种情况,两种球的总数超过99只”,若王五反面成立,则在这种情况下,三种球数量之和必然超过100只,不符合题干要求。因此,王五的话为真。
高能提示
本题也可一次性对三者“设特值”以验证:
因为总数为100只,并且三种球每种都得有,从而可取如下极端情况:33、33和34只;1、49和50只;1、1和98只。在第一种情况下,张三的话不成立,排除A、C和E项。而在这三种情况下,李四和王五的话都依然成立。因此,虽然“设特值”只能证伪不能证明,但对于选择题,可倾向于选B项。
题6 答案为A项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
复选项Ⅰ,因为撤销具有25%员工的三个机构后,仅减员15%。所以,不可能没有人员调动。若是最小的调动,也是要把原属于撤销机构的10%的员工,调入未撤销机构。因此,复选项Ⅰ必然成立,排除B项和C项。
复选项Ⅱ,若原属于撤销机构的25%的员工,均调入未撤销的某机构,再将10%原属于未撤销机构的员工,调入撤销机构。此时复选项Ⅱ反面成立,排除D项和E项。
根据效用思维(已知答案,其余不看),可不用验证复选项Ⅲ。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。复选项Ⅲ,根据效用思维(复用情况),复选项Ⅱ的情况恰好违背复选项Ⅲ。
题7 答案为E项。
注意本题的相反陷阱,寻找的是“除哪项外,都可能不违反”,即“必然违反”的选项。
A项,所提为“商用车”,与题干信息无关,因此可能为真,排除A项。
B、C和D项,若任意所提两台车之间尾号均不同组,则他们各自可以每天都开车,因此都可能为真,排除B、C和D项。
根据效用思维(已知答案,其余不看),可不用验证E项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
E项,一共六台车,必然有两台同组,从而在这两台车限号的时候,当天只会有四辆车可供使用,因此E项必然为假。
高能提示
本题也可“设特值”,找到符合B、C和D项的特殊情况,便可直接排除。
题8 答案为B项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
复选项Ⅰ,在第一句话为真时,若5个孩子有卵石,其数量分别为1、1、1、1和21,则第二句话并不成立,因此排除A、D和E项。
复选项Ⅱ,在第二句话为真时,因为卵石总数为25块,从而最多只能5个孩子有卵石,即第一句话为真,因此排除C项。
根据效用思维(已知答案,其余不看),可不用验证复选项Ⅲ。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。因为已知复选项Ⅱ为真,所以当第一句话为假时,第二句话必然为假,因此两者可以都为假。
题9 答案为C项。
观察题干发现,本题情况较多。因此,验证真假可采用“设特值”的方式。
复选项Ⅰ,可提炼为,∀双→当,是题干第一句的互换,真假不知,排除A、D和E项。
复选项Ⅱ,若下图情况成立,则复选项Ⅱ并不成立,排除B项。
上图中,“//”阴影表示可收到当代商厦购物奖券,“\\”阴影表示可收到双安商厦购物奖券。
根据效用思维(已知答案,其余不看),可不用验证复选项Ⅲ。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
复选项Ⅲ,根据题干第一句话可知,当持有当代商厦购物优惠卡的顾客数,等于持有双安商厦购物优惠卡的顾客数时,复选项Ⅲ中的数据可取到最值。若下图情况成立,则持有双安商厦购物优惠卡的顾客中,最多只有一半能收到当代商厦的购物奖券。
上图中,“//”阴影表示可收到当代商厦购物奖券,“\\”阴影表示可收到双安商厦购物奖券。
题10 答案为B项。
根据题干条件,可列出如下不等式:
10%×高二人数=高二成绩为优的人数>高一成绩为优的人数=10%×高一人数。
从而可知,高二人数多于高一人数。进而可知,高二成绩为差的人数多于高一成绩为差的人数,B项与其相符。
题11 答案为D项。
注意本题的相反陷阱,寻找的是“除了哪项外,都可能是”,即“必然不是”的选项。
题干所给条件,均是成为候选人的必要条件,从而可得出如下不等式组:
候选人数≤![]()
候选人数≤
候选人数≤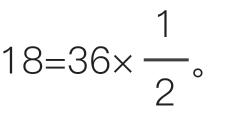
综上可知,候选人数≤9,D项与此违背。
题12 答案为B项。
复选项Ⅰ,因为“两人历史成绩相同”,所以必然为假,排除A项和D项。
复选项Ⅱ,因为李昌五门课程的平均成绩高于王平,并且两人历史成绩相同,所以根据数据运算的定性思维可知,去掉历史成绩后,李昌剩余四门课程平均成绩高于王平,所以必然为真,排除C项和E项。根据效用思维(已知答案,其余不看),可不用验证复选项Ⅲ。
题13 答案为A项。
根据题干条件,可列出如下等式及不等式组:
鲜纸浆2000年=2×回收纸浆2000年。
鲜纸浆2010年≤回收纸浆2010年。
鲜纸浆2000年<鲜纸浆2010年。
综上可得,2×回收纸浆2000年=鲜纸浆2000年<鲜纸浆2010年≤回收纸浆2010年。
从而可知,2×回收纸浆2000年<回收纸浆2010年。因此复选项Ⅰ为真,排除B项和C项。
复选项Ⅱ,且不谈题干尚未明确除鲜纸浆与回收纸浆外,是否还有其他纸浆。若鲜纸浆2010年产量仅略高于2000年,那么该项未必成立,因此排除D项和E项。
题14 答案为E项。
注意本题的相反陷阱,寻找的是“不为真”的选项。
因为两省基数相同,并且上涨与下降的比例和次数都相同。从而根据数据运算的定性思维可知,今年1—5月甲省的CPI比乙省高,而今年6月两省CPI相同,E项与此违背。
高能提示
当然,如果对数字并不敏感,难以使用定性思维,也可列出如下等式:
甲省今年6月CPI=甲省去年12月CPI×(1+0.018)3×(1-0.017)3。
乙省今年6月CPI=乙省去年12月CPI×(1-0.017)3×(1+0.018)3。
从而可知,甲省今年6月CPI=乙省今年6月CPI。
题15 答案为C项。
女性参加者的平均减肥量要比男性参加者更接近总体平均减肥量。因此,女性对平均值的影响要更大一些,所以根据数据运算的定性思维可知,女性的权重会更大一些,C项与其相符。
高能提示
当然,如果对数字并不敏感,难以使用定性思维,也可列出如下等式:
从而可知,
同时,本题也可运用管综数学十字交叉法(杨晶和聪聪老师多次强调),如下:
题16 答案为A项。
根据题干条件,可列出如下等式:
超标单位数=(1-80%)×总用户数=20%×总用户数。
不超标单位数=80%×总用户数。
上述两个公式结合可得,不超标单位数=4×超标单位数,所以复选项Ⅰ必然为真,排除B、C和D项。复选项Ⅱ和Ⅲ,是针对“耗电量”。但题干的意思是,将该地区的用电单位,按照日均耗电量大小排序,取前20%的作为超标单位。所以用电是否超标,仅看各用电单位之间的比较情况,与具体耗电量无关。因此
排除E项。
题17 答案为C项。
根据题干条件,可列出如下等式组:
肥胖儿童数=(1-80%)×总儿童数=20%×总儿童数。
非肥胖儿童数=80%×总儿童数。
上述两个公式结合可得,非肥胖儿童数=4×肥胖儿童数,C项与其相符。
题18 答案为C项。
根据题干条件,可列出如下等式:
A项,题干仅知甲公司员工数量相比去年是增加的,但并不知道去年相比前年的变化情况,因此真假不知,排除A项。
B项,在满足上述等式的前提下,会有如下特殊情况:甲公司员工数量增长1%,乙公司增长1 000%,丙、丁公司不增长(这里默认四家公司原来员工数量相等),此时丙、丁公司增长比例小于甲,排除B项。另外,根据效用思维(复用情况),此情况也可排除D项和E项。
C项,因为甲公司在员工数量增长的同时,上缴利润比例在下降,根据数据运算的定性思维可知,其余公司整体员工增长比例要更高,本项可由此推出。
题19 答案为D项。
根据题干背景,可列出如下夫妻中至少一人是中国人的相关情况:
由此表可知,每种情况均是丈夫数量等于妻子数量。根据题干条件,可得如下不等式:b+f>a+c。
复选项Ⅰ,所提数据为“单一数值”,而题干所提数据为“增加量”,是由“两个数值”所构成的数据,根据数据运算的定性思维可知,无法直接由其得到“单一数值”的情况,排除A和E项。
复选项Ⅱ,因为a=b,所以题干条件可变为,f>c,又因为f=e、c=d,从而e>d,所以一定为真,排除C项。
复选项Ⅲ,与中国人结婚的男性为a和e,与中国人结婚的女性为b和d,又因为a=b而e>d,从而a+e>b+d,所以一定为真,排除B项。
高能提示
因为丈夫与妻子数量相等,所以,本题还可根据两者至少一人是中国人的夫妻中,中国女性比中国男性多2万,直接定性得到,与他们结婚的人当中,外国男性比外国女性多2万。
题20 答案为D项。
根据题干背景,可列出如下与分居者相关的非法同居情况:
由此表可知,每种情况均是男性数量等于女性数量。根据题干条件,可得出如下不等式:b+f>a+c。
复选项Ⅰ,因为a=b,所以不等式可变为,f >c。又因为f=e、c=d,从而e>d,所以复选项Ⅰ一定为真,排除B项和C项。复选项Ⅱ,与分居者非法同居的人,即a、b、d和e。因为a=b,e>d,所以a+e>b+d,所以复选项Ⅱ一定为真,排除A项。复选项Ⅲ,与分居者非法同居的分居者,即a和b,但是a=b,所以一定为假,排除E项。
高能提示
因为男性与女性数量相等,所以,本题还可根据非法同居的分居者中,女性比男性多100万,直接定性得到,与他们同居的人当中,男性比女性多100万。
题21 答案为D项。
注意本题的相反陷阱,寻找的是“有助于解释结果”的选项,即推理方向是“下推上”。
复选项Ⅰ,如果本项为真,则只会造成分居者中,男性多于女性,无法解释题干结论,排除A项和E项。复选项Ⅱ和复选项Ⅲ,都表明本次普查中,男性数量少于实际数量,都可以解释题干结论,排除B项和C项。
高能提示
注意,本题不可以直接由结论推出非法分居者中女性比男性多100万。因为,如果统计过程有误,那么合法分居者中男性未必等于女性。
题22 没有答案,意图答案为D项。
注意本题的相反陷阱,寻找的是“错误”的选项。根据题干条件,可列出如下不等式组:
别墅均价:甲>乙>丙。
普通商用房均价:甲>丙>乙。
经济适用房均价:乙>甲>丙。
本题意图让考生在观察上述不等式后,发现一个共性——不论是哪种住房,甲城的均价都高于丙城,从而,根据数据运算的定性思维得出,必然甲城整体均价高于丙城均价,D项与此违背。
但实际上,本题并未限定三座城三种住房各自的占比面积。不妨设想一种极端情况,甲城的经济适用房占比面积无限趋近于1,别墅与普通商用房占比面积无限趋近于0;丙城别墅占比面积无限趋近于1,普通商用房与经济适用房占比面积无限趋近于0。此时,如果丙城别墅均价高于甲城经济适用房均价,那么甲城的整体均价会低于丙城。
故没有答案,意图答案为D项。
题23 没有答案。
住房整体均价,由三种住房各自均价和面积两个因素决定。因此,根据数据运算的定性思维可知,必然要把三种住房的“均价”“面积”都限定了,才能得出甲城整体均价最高的断定,因此排除A项和B项。
C项,根据效用思维(复用情况),可在上题特值的基础上稍加调整,如果甲城普通商用房占比面积无限趋近于1,别墅与经济适用房占比面积无限趋近于0;丙城别墅占比面积无限趋近于1,普通商用房与经济适用房占比面积无限趋近于0。根据数据运算的定性思维可知,如果丙城别墅均价高于甲城普通商用房均价,那么甲城的整体均价会低于丙城,排除C项。
复选项Ⅱ的含义为,三个城市各类住房之间比例相同,而不是每个城市各自三种住房占比都相同。因此,完全可以假设三座城市三种住房的比例都是1:1:18,此时根据数据运算的定性思维可知,哪怕复选项Ⅲ成立,也未必能改变乙比甲整体均价高的情况,排除D项。
E项,复选项Ⅰ和Ⅱ无法共存,排除E项。
高能提示
当然,如果对数字并不敏感难以使用定性思维,也可列出等式解题。
复选项Ⅱ,若三座城市的比例为1:1:18,从而可得如下等式:
从而可知:
复选项Ⅲ,若甲、乙两城之间,别墅房、普通商用房和经济适用房的差价分别为2、2和-1,此时依然是,乙整体均价高于甲。
另外,若把复选项Ⅱ改为“三座城市各自在售的别墅房、普通商用房、经济适用房占比面积都相同”,便可选D项。
题24 答案为C项。
A项和B项,所提数据均为“单一数值”,而题干所提数据为“增加量”和“占比”,均是由“两个数值”所构成的数据,根据数据运算的定性思维可知,无法直接由其得到单一数值的情况,所以排除A项和B项。
C项,由题干条件可构造如下情况:低收入的比例不变,而高收入的比例增加。此时,中等收入的比例确实有可能减少,因此,C项有可能为真。
注意,题目寻找的是“最可能得出”的选项,D项和E项有可能比C项更好,因此不能直接使用效用思维(已知答案,其余不看)。
D项,题干所言增加最多的是“首次就业人员数量”,而非“全体就业人员数量”,完全有可能其他低收入人员仅变成了“中等收入”,从而其所涉“相当数量”,相比于C项“有所减少”,过于夸张,因此,C项更可能为真。
E项,提及“经营实体”,此点没有题干依据。因此,其虽可能为真,但C项更好。
题25 答案为B项。
A项,提及“教学质量”,此点没有题干依据,故排除。
B项,验证起来比较烦琐,根据效用思维(不完全验证),可先跳过B项。
C、D和E项,所提数据均为“单一数值”,而题干所提数据为“占比”,是由“两个数值”所构成的数据,根据数据运算的定性思维可知,无法直接由其得到“单一数值”的情况,排除C、D和E项。
根据效用思维(已知答案,其余不看),可不用验证B项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
由题干两个占比,可得出如下等式组:
将两个等式相除可得:
所以,东江大学“全日制”学生数量所占总学生数的比例比西海大学的低,从而可得,东江大学“成人教育”学生数量所占总学生数的比例比西海大学的高。
题26 答案为D项。
A、B和E项,所提数据均为“单一数值”,而题干所提数据为“占比”,是由“两个数值”所构成的数据,根据数据运算的定性思维可知,无法直接由其得到“单一数值”的情况,排除A、B和E项。
C项,提及“可利用的农田”,此点没有题干依据,排除C项。
根据效用思维(已知答案,其余不看),可不用验证D项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
由题干两个占比情况,可得如下等式组:
将两个等式相除可得:
题27 答案为C项。
A项,题干未给出“会议主席”关于“认识组员”的条件,排除A项。
B项,题干已给出组员之间“有认识的”,排除B项。
C项,“可能”不是绝对化的词,因此排除较为困难,根据效用思维(不完全验证),可暂且跳过。
D项,题干未给出认识的“程度”,排除D项。
E项,题干未给出“未来”的情况,排除E项。
根据效用思维(已知答案,其余不看),可不用验证C项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
题干给出“一人认识小组中三人、三人认识小组中二人和四人认识小组中一人”,从而可知,认识总数=1×3+3×2+4×1=13,为奇数。然而,如果题干所提认识均是互相认识,则认识总数应为偶数。所以,至少有一个人的认识仅是单方认识,因此C项可能为真。
题28 答案为A项。(https://www.xing528.com)
根据题目中的“常春藤毕业生”可定位题干最后四个条件。前两个条件不仅涉及范围广,且均提及“大多数”,所以根据数据运算的定性思维可知,两者描述的内容必然有交集,从而结合后可得,有的社会精英年薪超过20万美元。
高能提示
本题也可根据数据运算的定性思维,做以下排除:
后两个条件中“有很多”“为数众多”的定义不清——1 000个算不算多?100个算不算多?更难以知晓其占总体的比例有多少,万一常春藤毕业生有1个亿,那么不论是1 000还是100均是极小的一部分。从而,这两个条件难与前面条件联立,排除B、C、D和E项。
题29 答案为E项。
题干所给三个数据均为比值,前两个数据的分母为“‘希望之星工程’的捐款”。并且,第一个数据为82%,第二个数据为25%,两者相加后大于1,所以根据数据运算的定性思维可知,两者分子必然有交集,即“200家年盈利一亿元以上的大中型企业”与“民营企业”必有交集,E项与其相符。
题干前两个数据针对的是“捐款额”,而最后一个数据针对的是“企业数量”,所以并不能由题干数据判断两者具有交集,所以B项不可入选。
题30 答案为B项。
题干条件中,明显存在以总人数为自变量的规律,从而可使用“归纳法”:
设总人数为1,因每人论文数不同且不超过人员总数,所以每人发表论文数为0。
设总人数为2,因每人论文数不同且不超过人员总数,所以每人发表论文数为0,1。
设总人数为3,因每人论文数不同且不超过人员总数,所以每人发表论文数为0,1,2。
从而发现,当总人数为n,每人发表论文数为0,1,2,……,n-1。
再加上还未使用的条件——没有人恰好发表了10篇论文,可知必须满足:n-1<10,则n<11。
因此复选项Ⅰ和复选项Ⅲ必然为真,复选项Ⅱ不一定为真,从而排除A、C、D和E项。
题31 答案为B项。
“哈尔滨”属于“北方”,所以“一个哈尔滨人”与“两个北方人”是重叠的。
若要人数最多,让剩余条件不重叠即可,所以人数最多为2+1+2+3=8人,排除C项。
若要人数最少,让剩余条件尽量重叠即可。因为“北方”和“广东”不可能重叠,所以从地域来看,最少3人;因为“只做电脑生意”和“只做服装生意”不可能重叠,所以从职业来看,最少5人。但是,地域和职业是可以重叠的,因此总人数最少5人,排除A项和D项。
题32 答案为B项。
“大连”属于“北方”,所以“一个大连人”与“两个北方人”是重叠的。
若要人数最多,让剩余条件不重叠即可,所以人数最多为2+1+2+3=8人,排除C项和D项。
若要人数最少,让剩余条件尽量重叠即可。因为“北方”和“云南”不可能重叠,所以从地域来看,最少3人;因为“只选修了逻辑哲学”和“只选修了古典音乐欣赏”不可能重叠,所以从专业来看,最少5人。但是,地域和专业是可以重叠的,因此总人数最少5人,排除A项。
题33 答案为C项。
本题虽然有多种情况,但题目所问为“最少”邀请人数。因此,尽量让所提人物身份重叠即可。而“父亲的姐夫”“姐夫的父亲”“岳母的哥哥”均为男性,因此可以重叠,从而邀请的最少人数为2人。
高能提示
其实,本题命题稍有不严谨,争议答案为D项。若画出族谱,则可得情况如下:
从而可知,如果“父亲的姐夫”和“姐夫的父亲”重叠,便说明,“我”姑姑的儿子(“我”的表哥)娶了“我”的姐姐。
但如果真的这么思考,且不说画族谱会非常麻烦、耗时,联考大纲规定不考查专业背景知识,此伦理知识有属于专业背景的可能,所以本题选C项。
题34 答案为B项。
注意本题的相反陷阱,寻找的是“都有可能加强,除了”,即“必然不加强”的选项。
“哈尔滨”属于“北方”,所以“一个哈尔滨人”与“两个北方人”是重叠的,从而剩下的数字之和恰好为8(2+1+2+3=8)。因此,要想题干断定成立,必须确保两点:第一,上述条件已经描述了宿舍中的所有人;第二,上述条件之间不会重叠。
A项,确保了第一点,排除A项。
B项,表明该宿舍的“广东”与“法律系”重叠,则违反第二点。
根据效用思维(已知答案,其余不看),可不用验证其余选项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
C项,题干没有提及“财经系”,因此不与题干信息违背。
D项,即使进修生都是“南方人”,也未必与“广东人”重叠,因此不与题干信息违背。
E项,表明“法律系”不会与“进修生”重叠,确保了第二点。
题35 答案为C项。
注意本题的相反陷阱,寻找的是“都不与题干矛盾,除了”,即“必然矛盾”的选项。
“哈尔滨”属于“北方”,所以“一个哈尔滨人”与“两个北方人”是重叠的,从而剩下的数字之和恰好为8(2+1+2+3=8)。因此,要想题干断定成立,必须确保两点:第一,上述条件已经描述了宿舍中的所有人;第二,上述条件之间不会重叠。
A项,表明“法律系”有可能与“进修生”重叠,但不代表该宿舍的人会重叠,因此不与题干信息矛盾,排除A项。
B项,表明“法律系”不会与“进修生”重叠,确保了第二点,排除B项。
C项,表明该宿舍的“广东“与“法律系”重叠,则违反第二点。
根据效用思维(已知答案,其余不看),可不用验证其余选项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
D项,题干没有提及“财经金融系”,因此不与题干信息违背。
E项,即使进修生都是“南方人”,但未必与“广东人”重叠,因此不与题干信息违背。
题36 答案为A项。
注意本题的相反陷阱,寻找的是“都与题干不矛盾,除了”,即“必然矛盾”的选项。
“大连”属于“北方”,所以“一个大连人”与“两个北方人”是重叠的,从而剩下的数字之和为8(2+1+2+3=8)。但题干表明总人数为7人,因此,要想确保此点成立,上述条件之间必然有且只有1人重叠。
A项,表明委员中,两个“特长生”都与“贫困生”重叠,违反上述要求。
根据效用思维(已知答案,其余不看),可不用验证其余选项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
B项,表明“北方”与“贫困生”重叠,因此不与上述要求矛盾。
C项,即使特长生都是“南方人”,但题干仅说了一个南方人,因此不与上述要求矛盾。
D项,表明委员中存在一个“大连人”与“特长生”重叠,因此属于上述要求之内。
E项,题干中“福州人”的其他身份可以未被描述,因此不与上述要求矛盾。
题37 答案为D项。
因为是循环赛,所以每队都会打3场比赛。从而可知:第一名是3胜0负;第二名是2胜1负;第三名是1胜2负;第四名是0胜3负。
因为B队输掉1场,所以B队是第二名,排除B项。因为C队比B队少赢一场,所以C队是第三名,排除C项。因为B队比D队少赢一场,所以D队是第一名,排除A项。
题38 答案为A项。
根据题干所给条件,可得表格如下:
观察选项后发现,四个选项均涉及“投资第三产业外资”和“投资非第三产业内资”。
设投资第三产业的外资为a,从而可知,投资非第三产业的外资为5.7-a,投资第三产业的内资为4.6-a,投资非第三产业的内资为a-0.3,A项与其相符。
题39 答案为B项。
根据题干信息,可得表格如下:
再由题干所给条件,可得出如下不等式组:a+b>c+d、b+d>a+c。两式相加可得,a+2b+d>a+2c+d,进而可知,b>c,复选项Ⅲ与其相符。其余内容均不可知。
题40 答案为A项。
题干所给条件为:有花植物占大多数;阔叶树种超过半数;珍稀树种超过一般树种。
因为后两个条件有重复项,所以优先联立,可得表格如下:
从而根据此两个条件,可得如下不等式组:a+b>c+d、a+c>b+d。两式相加可得,2a+b+c>b+c+2d,进而可知,a>d,A项与其相符。
高能提示
本题也可根据数据运算的定性思维,做以下排除:
题干第一个条件中的“植物”与后两个条件中的“树种”是两个概念,虽然后者归属于前者,但不可直接将第一个条件与后两个条件联立,因此排除B项和E项。
C项中的“挂果”、D项中的“采摘”,题干均未提及,因此排除C项和D项。
题41 答案为B项。
设连队总人数为n(100<n<200),从而由题干条件可得出如下等式组:n=5x+1;n=7y+1;n=8z+2。
变形后可得:n-1=5x;n-1=7y;n=2×(4z+1)。
从而可知,n-1是5和7的公倍数。因此,结合100<n<200可知,n-1可能的取值范围是105、140和175,从而n可能的取值范围是106、141和176。
再由第三个等式可知,n必然为偶数,进而n可能的取值范围缩小为106和176。将106和176代入第三个等式可知,106可被整除,而176无法被整除,因此连队人数只能是106人,则除连长外,正好排成三列横队。
题42 答案为A项。
根据题干条件,可得出如下等式组:
雌=雄-1-1。
雄=2×(雌-1)-2。
两式结合,解方程组后可得,雄=8,雌=6。A项与其相符。
管综真题警戒线
题43 答案为E项。
题干信息较多,可用选项来定位题干条件。
观察选项后发现,C项和D项是“2006年”,而题干是“2007年”,排除C项和D项。A项是“西方国家”,题干并未提及,排除A项。B项是“比较中国与其他国家的生活质量指数”,但题干中并无中国与其他国家的比较,排除B项。E项针对“挪威”,定位题干第一句话“挪威是世界上居民生活质量最高的国家”,E项与其相符。
题44 答案为D项。
题干信息较多,可用选项来定位题干条件。
观察选项后发现,多数选项围绕“2015年卷烟消费量下降比率”。因此先定位于“2015年中国卷烟消费量下降了2.4%”“2015年全球卷烟消费量下降了2.1%”。
由上述条件,根据数据运算的定性思维可知,其他国家卷烟消费量的下降比率拖了中国的后腿,从而使得世界数据低于中国,C项与此违背,D项与其相符。E项的“发达国家”,题干并未提及。
根据效用思维(已知答案,其余不看),可不用验证其余选项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
A和B项,围绕“2013、2015年中国卷烟消费量的比较”,因此可定位于“2014年中国卷烟消费量上升2.4%”“2015年中国卷烟消费量下降了2.4%”。2014年上升和2015年下降的比例,都是对应上年的2.4%,但是2015年下降的基数是2014年的量,2014年上升的基数是2013年的量。根据数据运算的定性思维可知,必然可知2015年下降的量要比2014年上升的量大,从而可知2015年的数据应该是小于2013年的。
高能提示
当然,如果对数字并不敏感,难以使用定性思维,也可列出等式解题。
对于C和D项,因为“2015年中国卷烟消费量占全球的45%”,运用管综数学十字交叉法(杨晶和聪聪老师多次强调),设其他国家卷烟消费量为x,从而可得出如下等式:
解等式后可得x≈1.85。
对于A和B项,可得出如下等式:
2015年量=2014年量×(1+0.024)=2013年量×(1-0.024)×(1+0.024)=2013年量×(1-0.0242)
题45 答案为B项。
注意本题的相反陷阱,寻找的是“与上述信息相冲突”的选项。
A项,“略有增长”在“持续增长”范畴之内,因此不与题干信息冲突,排除A项。
B、D和E项,都是关于“笔记本电脑销量占公司总销量的比例”,根据效用思维(复用情况),可一起分析。因为笔记本电脑的增长率比整个公司的低,即笔记本电脑的增长要比其他产品慢,所以根据数据运算的定性思维可知,笔记本电脑销量所占公司总销量的比例,应该下降。因此,B项与题干信息违背,D项和E项不与题干信息冲突。
根据效用思维(已知答案,其余不看),可不用验证C项。
高能提示
当然,如果对数字并不敏感,难以使用定性思维,也可列出如下等式:
乘号左边分式为常数,右边分式小于1,因此笔记本电脑占比是下降的。
题46 答案为E项。
因为甲校本科生的人均经费投入低于乙校,但甲校全校的人均经费投入却高于乙校,根据数据运算的定性思维可知:或者是甲校本科生占比更少,从而降低了其本科生的数据劣势;或者是甲校研究生人均经费更高,从而用研究生的数据优势,抵消了本科生的数据劣势。E项与之相符。
高能提示
当然,如果对数字并不敏感,难以使用定性思维,也可列出如下等式:
全校人均经费=本科生人均经费×本科生占比+研究生人均经费×研究生占比。
其等价于:全校人均经费=本科生人均经费×(1-研究生占比)+研究生人均经费×研究生占比。因为甲校本科生人均经费低于乙校,所以要想全校人均经费扭转,只能靠剩余因素。
本题不论是看性质,还是列公式,都比较烦琐。但选项的答案特征很明显——C项和D项就是E项的拆分,也就是说,C项或D项任意一个是答案,E项就一定是答案。所以当年本题,很多人都做对了。
题47 答案为D项。
题干条件中,明显存在干与支的规律——既有干对支的轮回,也有支对干的轮回,从而。可使用“归纳法”。
先看干对支的轮回。根据题干所给“天干配地支”的规律,可得甲第一次出现在“子”上面,第二次出现在“戌”上面,但仅凭出现两次,很多小伙伴们难以发现规律。因此可再数一次,从而可得第三次甲出现在“申”上面,从而可得出下表:
再看支对干的轮回。根据题干所给“天干配地支”的规律,可得子第一次出现在“甲”下面,第二次出现在“丙”下面,但仅凭出现两次,很多小伙伴们难以发现规律。因此可再数一次,从而可得第三次子出现在“戊”下面,从而可得出下表:
由此便可找出轮回规律:干每隔10年出现一次,都是在支的上面往前顺两位;支每隔12年出现一次,都是在干的下面往后顺两位。下面验证选项。
A项,根据上述循环规律,甲永远不会在“丑”上面出现,排除A项。其实,本项也可根据数据运算的定性思维加以排除,因为天干和地支在配的时候,永远都是奇数位的干配奇数位的支,偶数位的干配偶数位的支。而“甲”属于奇数位,“丑”属于偶数位,所以两者永远不会相配。
B项中的“现代人”、C项中的“农事”,题干均未提及,故排除。
D项,因为60年为一完整循环,既然2015年是乙未年,那么2075年也是乙未年。而2087年与2075年间隔12年,所以2087年的支还是“未”。然后,让支在干下面往后顺两位,从而2087年的干是“丁”。
根据效用思维(已知答案,其余不看),可不用验证E项。为减少疑惑,此处特做分析,但小伙伴们要明白,这样非常不应试。
E项,既然2014年是甲午年,而2024年与2014年间隔10年,所以2024年的干还是“甲”,让干在支上面往前顺两位,从而2024年的支变为“辰”。
高能提示
题干有完整的天干和地支,因此考试时,可直接在上面推算轮回规律,无需列出表格。
题48 答案为A项。
根据题干所给条件,可得表格如下:
设G区常住外来人口为a,则G区户籍人口为240-a,H区常住外来人口为200-a,进而可知,H区户籍人口为a,A项与其相符。
题49 答案为E项。
题干条件中包含总人数,以及总人数下的其他数据,从而有暗示考生做减法的迹象。按照这个思路,可依次得出如下减法传递:
60(总人数)-31(亚裔学者)=29(非亚裔学者)。
29(非亚裔学者)-4(非亚裔学者∧无博士)=25(非亚裔学者∧博士)。
33(博士)-25(非亚裔学者∧博士)=8(亚裔学者∧博士)。
高能提示
本题也可采用列表的方式,思路也是上述的“减法传递”。具体表格如下:
其中,非斜体数字为题干所给条件,斜体数字为传递后所得内容。
题50 答案为B项。
题干条件中包含总人数,以及总人数下的其他数据,从而有暗示考生做减法的迹象。按照这个思路,可依次做出如下减法传递:
385(总人数)-189(女生)=196(男生)。
196(男生)-41(男生∧文科)=155(男生∧理科)。
因为非应届男生包含了非应届文科男生,也包含了非应届理科男生。所以,无法直接去“理科男生”。又因为,“非应届理科男生”可直接减理科男生,因此设“非应届文科男生”人数为a,从而“非应届理科男生”人数为28-a。
然后可继续向下传递:
155(男生∧理科)-[28-a(男生∧理科∧非应届)]=127+a(男生∧理科∧应届)。
256(理科∧应届)-[127+a(男生∧理科∧应届)]=129-a(女生∧理科∧应届)。
因为a≥0,所以女生∧理科∧应届≤129。
高能提示
本题也可采用画图的方式,思路也是上述的“减法传递”。具体的图如下:
其中,非斜体数字为题干所给条件,斜体数字为传递后所得内容。不过画图后,连续的传递思路会被打断,且会造成考生有一种填完所有空的感觉。因此,画图的方法反而不应试。
题51 答案为E项。
根据题干条件,可得出如下不等式组:
(1)女青师≥5;(2)女中师≥6;(3)女青师≥7。
条件(1)和(3)描述的都是“女青师”,因为满足条件(3)必然满足条件(1),从而仅需考虑条件(2)和(3)。又因为,“女青师”与“女中师”虽然为两个概念,但都归属于“女师”,从而可知,“女师”必然大于等于13人,E项与其相符。
题52 答案为D项。
题干所给条件为:
(1)三个年级人数相等。(2)全部一年级:名句、诗名与作者都能对应。(3)2/3二年级:名句与作者能对应⇔1/3二年级:名句与作者不能对应。(4)1/3三年级:名句与诗名不能对应⇔2/3三年级:名句与诗名能对应。
A和E项,题干针对二、三年级的描述分别不涉及“诗名”“作者”,但A项描述了全校关于“名句”“诗名”“作者”同时对应的情况,因此无法得出;同理,E项也无法得出。因此,排除A项和E项。
B项,因为二年级有1/3的人不能把名句与作者对应,三年级有1/3的人不能把名句与诗名对应,而三个年级人数相等。因此,一共有(1/3+1/3)÷3=2/9的硕士生不能把名句与作者或诗名对应,排除B项。
C项,因为一年级都能把名句与作者对应,二年级有1/3的人不能把名句与作者对应,而三个年级人数相等。因此,一共有(0+1/3)÷2=1/6的一、二年级学生不能把名句与作者对应,排除C项。
D项,因为一年级都能把名句与诗名对应,三年级有2/3的人能把名句与诗名对应,而三个年级人数相等。因此,一共有(1+2/3)÷2=5/6的一、三年级学生能把名句与诗名对应。
题53 答案为C项。
设4个年级的参赛人数分别为a、b、c和d(a+b+c+d=12)。
结合条件(3),不妨设a×b=c,可用假设法:
若a=1,则b=2,c=2,违背条件(2)。
若a=2,则b=3,c=6,进而得d=1,此时不违背任何条件,是可能存在的情况。
若a=3,则b=4,c=12,违背条件(1)。
因为再往下假设a的数值,便会使得总人数超过12人。因此,a=2、b=3、c=6、d=1是满足题干条件的唯一情况,此时最多的人数是6。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




