数据分析：柘荣太子参产业化影响因素与产业化水平的相关关系

4.4.1　相关分析

本部分主要是采用Person相关分析法，进行双侧显著性检验来判断“柘荣太子参”产业化影响因素与产业化水平及“柘荣太子参”产业化影响因素之间的相关关系，初步判断本章所提出的研究假设的基本状况。

通过表4-19（a）的结果表明中介组织收益和合同遵守程度与其他影响因素相关比较强，以及种植收益和种植成本与其他影响因素相关也比较强，其他各自变量之间基本上不存在高度相关。

表4-19（a）　相关性

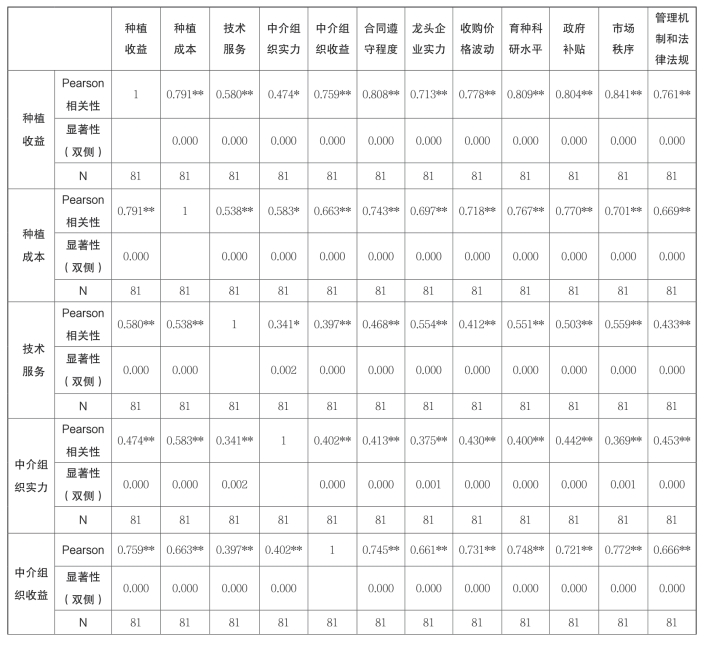
（续 表）

**.在0.01水平（双侧）上显著相关

表4-19（b）　相关性

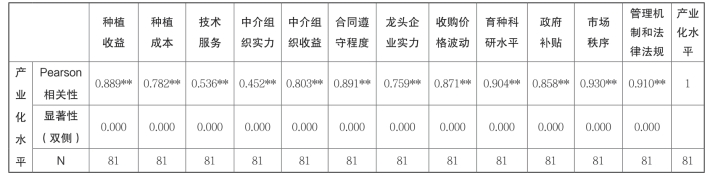
从表4-19（b）可知，“柘荣太子参”产业化各影响因素与产业化水平的关系中，种植收益、种植成本、技术服务、中介组织实力、中介组织收益、合同遵守程度、龙头企业实力、收购价格波动、育种科研水平、政府补贴、市场秩序管理机制和法律法规及产业化水平存在正相关关系（p＜0.01），且相关系数分别为0.889、0.782、0.536、0.452、0.803、0.891、0.759、0.871、0.904、0.858、0.930、0.910、1；通过以上分析和表4-19（b）的结果，初步验证了“柘荣太子参”产业化影响因素与产业化水平之间相关关系的假设模型。

4.4.2　回归分析

本部分在相关分析的基础上，进一步考察变量之间因果关系，主要的思路是，先采用强迫进入多元回归分析，得到全部的影响因素自变量与产业化水平因变量的回归模型，然后再用逐步回归分析方法建立影响因素与产业化水平之间的最终的回归方程，通过各影响因素对产业化水平的回归分析对模型的假设关系进行验证。

（1）回归模型的检验

本章主要针对多元线性回归的三大基本问题来对回归模型进行检验，判断样本数据是否符合回归分析的要求。

① 多重共线性

多重共线性是指一个或者多个自变量与其他自变量有线性关系。吴明隆（2010）指出可用容忍度（tolerance）、方差膨胀因子（VIF）和条件指针（CI）来判断变量间是否存在多重共线性[81]。一般而言，VIF介于0到10区间内表明回归模型不存在共线性问题；VIF介于10到100区间内，表明回归模型存在较强的共线性问题。容忍度是VIF的倒数其在0到1的区间内，越接近0，表示VIF越大，表明变量之间存在着很强的共线性。本章选取容忍度和方差膨胀因子作为判断回归模型是否存在共线性的指标。

② 序列相关

序列相关是回归模型中的不同的残差项之间具有相关关系。本章通过判断回归模型中的Durbin-Watson值（DW值）来检验模型的序列相关问题，检验的标准是：如果DW值在1.5至2.5的区间内（或者接近于2），那么可以判断误差项之间不存在自相关的现象。

③ 异方差

异方差是指因变量随着自变量的变化，方差存在明显的变化趋势，即模型中的不同的残差项之间具有不同的方差。本章利用散点图分布规律来判断回归模型是否存在异方差的现象。

（2）多元回归分析

本章先使用强迫进入的回归分析方法，将所有影响因素变量全部进入回归模型，分析本章先前建立的模型及提出的各项假设的验证情况，之后采用逐步回归分析法，确定最终的回归方程。

由表4-20（a）分析结果可知，所有变量的VIF值分布在1.626到9.560的区间内，均小于临界值10，因此可以判断回归模型不存在共线性的问题；由表4-20（b）所示，DW检验值为2.030，介于1.5到2.5的区间内且非常接近2，表明误差项之间不存在序列相关的现象，误差项基本上是独立的；通过以上分析可知，本章的回归模型通过检验。(www.xing528.com)

表4-20（a）　回归系数与显著性系数检验表a

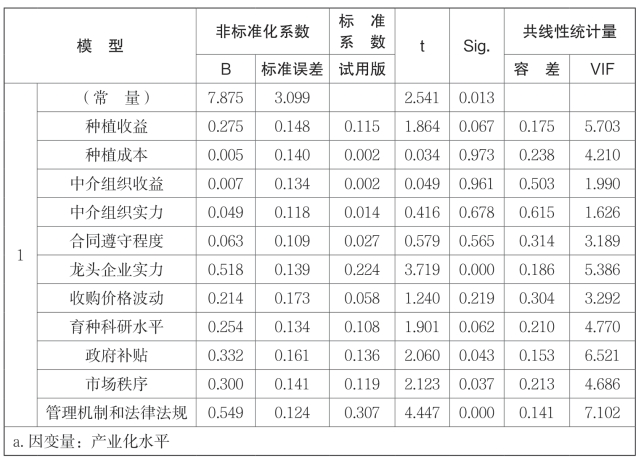
表4-20（b）　模型汇总

由表4-20（b）可知调整的判定系数R2为0.946，与1很接近，表明模型的拟合优度很高，回归模型很大程度上解释了因变量产业化水平。由表4-20（c）结果显示：F统计量为131.522，概率P值为0.000，小于0.001，线性回归方程具有显著性，可以拒绝偏回归系数同时为零的假设。因此，因变量与自变量的线性关系显著，可用线性模型来描述产业化水平与各影响因素之间的关系。

表4-20（c）　Anova

由表4-20（a）可以建立如下线性回归方程：

产业化水平＝0.115×种植收益+0.002×种植成本+0.002×技术服务+0.14×中介组织收益+0.027×中介组织实力+0.224×合同遵守程度+0.058×龙头企业实 力+0.108×收购价格波动+0.136×育种科研水平+0.119×政府补贴+0.307×市场秩序+0.099×管理机制和法律法规

但是在显著性水平为0.05的条件下，除了合同遵守程度、育种科研水平、政府补贴、市场秩序、法律法规外，剩余的变量的回归系数显著性检验的概率P值都大于0.05，表示这些变量的偏回归系数和0没有显著差异，与因变量的线性关系不显著，应该从方程中剔除。下面采用逐步回归方法重新确立回归方程。逐步回归分析的结果如表4-21所示。

表4-21（a）　模型汇总

从表4-21（a）可知，经过了七步完成回归方程的建立，得到的第七个模型为最终确定的模型。在逐步回归的过程中方程的拟合优度逐渐提高，同时自变量对因变量的解释量也在提高。

表4-21（b）　Anova

（续 表）

表4-21（c）　回归系数与显著性系数检验表a

（续 表）

表4-21（b）中的第七个模型是最终的方程，模型中的F统计量为243.854，概率P值为0.000，小于0.001，线性回归方程具有显著性。因此被选入的影响因素与产业化水平之间具有显著的线性关系。根据表4-21（c）可以确定最终的回归方程是：

产业化水平＝0.310×市场秩序-0.205×合同遵守程度+0.105×政府补 贴+0.101×管理机制和法律法规+0.122×种植收益+0.123×育种科研水 平+0.103×收购价格变动。