滑坡稳定性计算及应用方法简介

8.2.3　滑坡稳定性计算

滑坡稳定性计算是滑坡稳定性评价的基础。滑坡稳定性计算应符合下列要求:

（1）正确选择有代表性的分析断面，正确划分牵引段、主滑段和抗滑段；

（2）正确选择强度指标，宜根据测试成果、反分析和当地经验综合确定；

（3）有地下水时，应计入浮托力和水压力；

（4）根据滑面（带）条件，按平面、圆弧或折线，选用正确的计算模型；

（5）当有局部滑动可能时，除验算整体稳定外，尚应验算局部稳定；

（6）当有地震、冲刷、人类活动等影响因素时，应计入这些因素对稳定的影响。

在滑坡稳定性计算中，极限平衡理论计算方法、有限元数值模拟法、概率法等已经取得了很多有价值的计算成果，并已成功地应用于滑坡的整治工程。以下主要介绍刚体极限平衡法中的几种常用方法。

极根平衡理论是岩体力学、土力学的重要理论，应用该理论，分析、计算特定条件下各类斜坡的整体稳定系数F_s，当F_s大于等于滑坡稳定安全系数Fst（F_st＝1.05～1.5）时，滑坡可认为是整体稳定的。

1.滑动面为单一平面

当岩质边坡的主要结构面走向平行于坡面走向，结构面倾角小于坡角且大于其内摩擦角时，易发生平面破坏（如图8-4所示）。

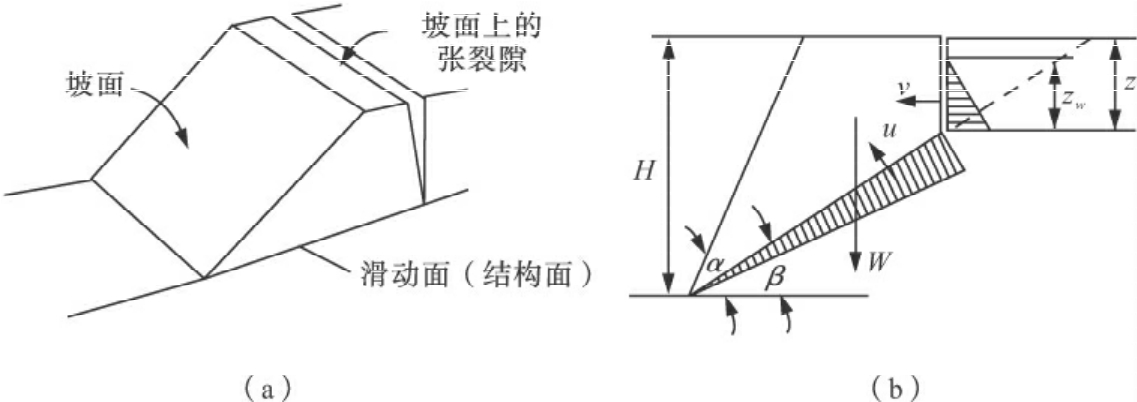
图8-4　坡面上有张裂隙的岩质边坡的平面破坏分析图

（a）立体图；（b）剖面图

整体稳定系数F_s可按下列公式计算:

式中:γ_w——水的重度，kN/m³；

γ——岩体的重度，kN/m³；

α——坡角，°；

β——结构面倾角，°；

W——滑体的重力，kN；

C、φ——结构面物质黏聚力（kPa）和内摩擦角（°），用直接快剪或三轴不排水剪试验求

得。

2.滑动面为圆弧形

对于均匀土质边坡及节理发育的岩体或弃石堆边坡，易发生转动破坏，滑面呈圆弧形（图8-5），常采用条分法，可按总应力法或有效应力法计算稳定系数。

（1）当假定条块两侧的作用力大小相等，方向相反且作用于同一直线上时，用瑞典条分法计算。

按总应力法时，稳定系数按下式计算:

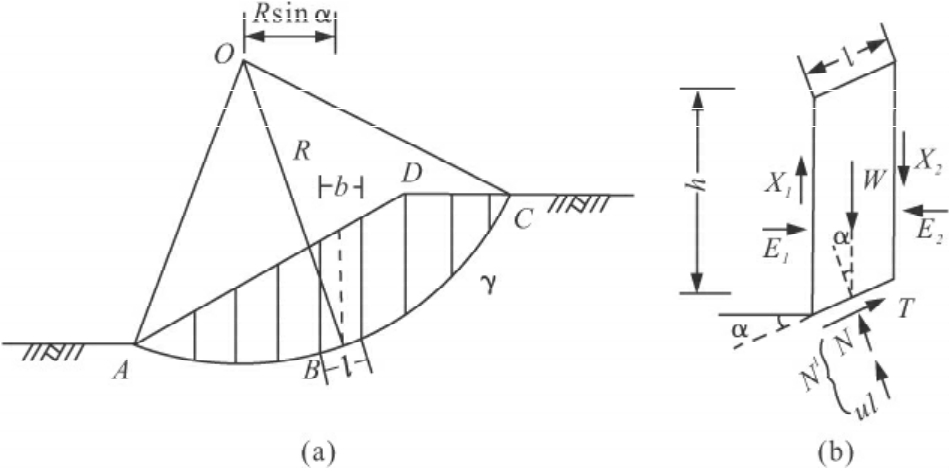
图8-5　均质边坡中圆弧形滑动面稳定性分析图

式中:N——分条条块重量垂直于潜在滑面的分量，kN/m；

C、φ——斜坡物质的黏聚力（kPa）和内摩擦角（°），用直接快剪或三轴不排水剪试验求

得；

l——潜在滑弧长度，m；

T——分条条块重量平行潜在滑面的分量，kN/m。

（2）按有效应力法时，稳定系数可按下式计算:

式中:u——斜坡中孔隙水压力，kPa；

C′、φ′——斜坡物质有效黏聚力（kPa）和有效内摩擦角（°），用直接快剪或三轴不排水剪

试验求得。

其他符号意义同上。

3.滑动面呈楔形

当岩质边坡的两组结构面的交线倾向坡面、交线倾角小于坡角且大于其内摩擦角时，易发生楔形破坏，滑动面为楔形，楔体沿结构面交线下滑（如图8-6所示）。

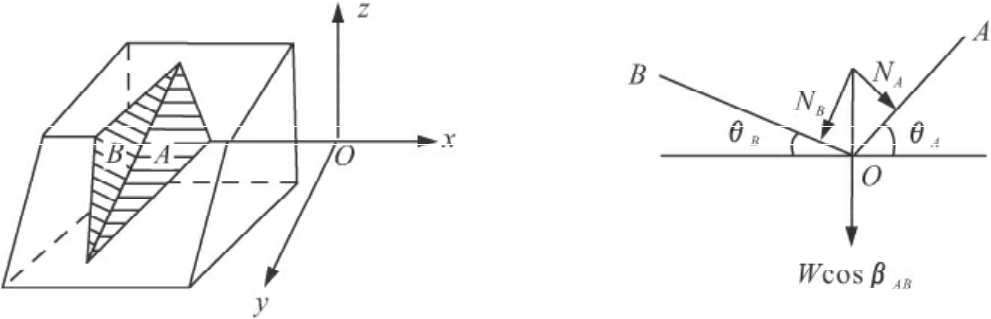
图8-6　滑动面为楔形的稳定性分析示意图

（a）楔体的分解分析图；（b）楔体夹角

稳定系数可按下式计算:(www.xing528.com)

式中:NA、NB——由W引起的作用于结构面A、B上的法向力，kN；

φA、φB——结构面A、B的内摩擦角，°；

CA、CB——结构面A、B的黏聚力，kPa；

AA、AB——结构面A、B的面积，m²；

W——楔体的重力，kN；

βAB——A、B结构面交线的倾角，°。

需要注意的是:当边坡中有地下水活动或边坡位于强震区，以及边坡上有荷载作用时，稳定系数的计算应考虑到静水压力、动水压力和水平地震力的影响。

4.滑动面为折线

当滑动面不规则时，可根据所查明的滑动面起伏情况，划分为折线形滑面（图8-7），按下列公式计算其稳定系数:

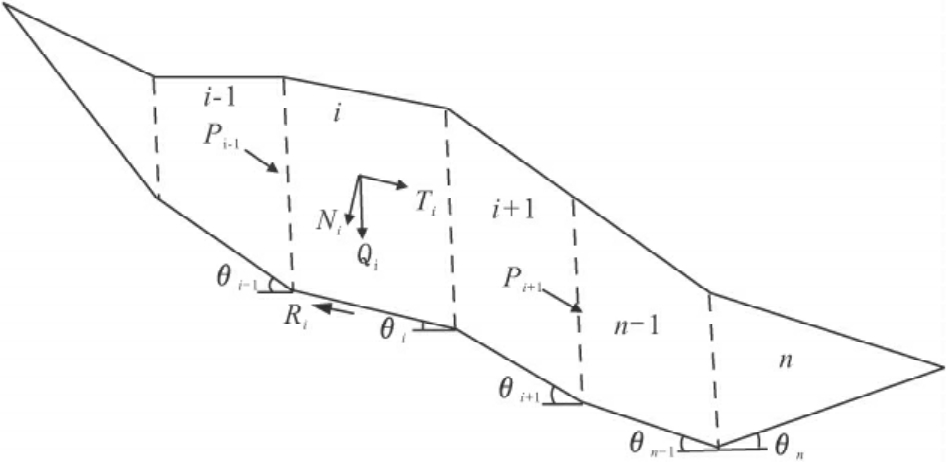
图8-7　滑坡稳定系数计算示意图

式中:F_s——稳定系数；

Q_i——第i块段滑体的重力，kN/m；

R_i——作用于第i块段的抗滑力，kN/m；

Ni——第i块段滑动面的法向分力，Ni＝Q_icosθ_i，kN/m；

φi——第i块段土的内摩擦角，°；

C_i——第i块段土的黏聚力，kPa；

l_i——第i块段滑动面长度，m；

T_i——作用于第i块滑动面上的滑动分力（kN/m），T_i＝Q_isinθ_i，出现与滑动方向相反的

滑动分力时，T_i应取负值；

ψj——第i块段的剩余下滑力传递至i＋1块段时的传递系数（j＝i）。

采用刚体极限平衡方法验算滑坡的稳定性时，除分情况计算滑坡的稳定系数F_s，进行整体验算外，还应视具体情况验算局部滑动的可能性。

此外，在滑动面（带）为折线时，应选择平行方向的断面（不宜少于3个，其中应有一个是主滑断面）计算滑坡推力，并根据不同断面的计算推力值设计相应的抗滑结构。滑坡推力一般按传递系数法计算，用下列公式:

式中:P_i、P_i-1——第i块、第i-1块滑体的剩余下滑力，kN/m；

F_st——滑坡稳定安全系数，应根据滑坡现状及其对工程的影响等因素确定，宜取1.05～1.25。

其余符号意义同上。

滑坡推力作用点，宜取滑体厚度的1/2处。

5.Sarma法

该方法的基本思路是:除非边坡岩体是沿一个理想的平面或圆弧面滑动，才可以作为一个完整的刚体运动。否则，岩土体必须先破裂成多块可相对滑动的块体，即在滑体内部发生剪切破坏才可能滑动。

该方法的独特优点是:①它可以用来评价各种类型滑坡的稳定性，计算时同时考虑滑体底面和侧面的抗剪强度参数，且各滑块可具有不同的C、φ值；②滑块的两侧可以任意倾斜，并不仅限于竖直边界，因而能分析具有各种结构特征的滑坡稳定性；③由于引入了临界水平加速度判据，因此该方法还可以用来分析地震对斜坡稳定性的影响。许多工程分析实例表明，Sarma法能比较全面客观地反映斜坡的实际情况，计算结果与实际情况拟合较好。

Sarma法的滑块力学模型及几何尺寸如图8-8所示。其平衡条件为:

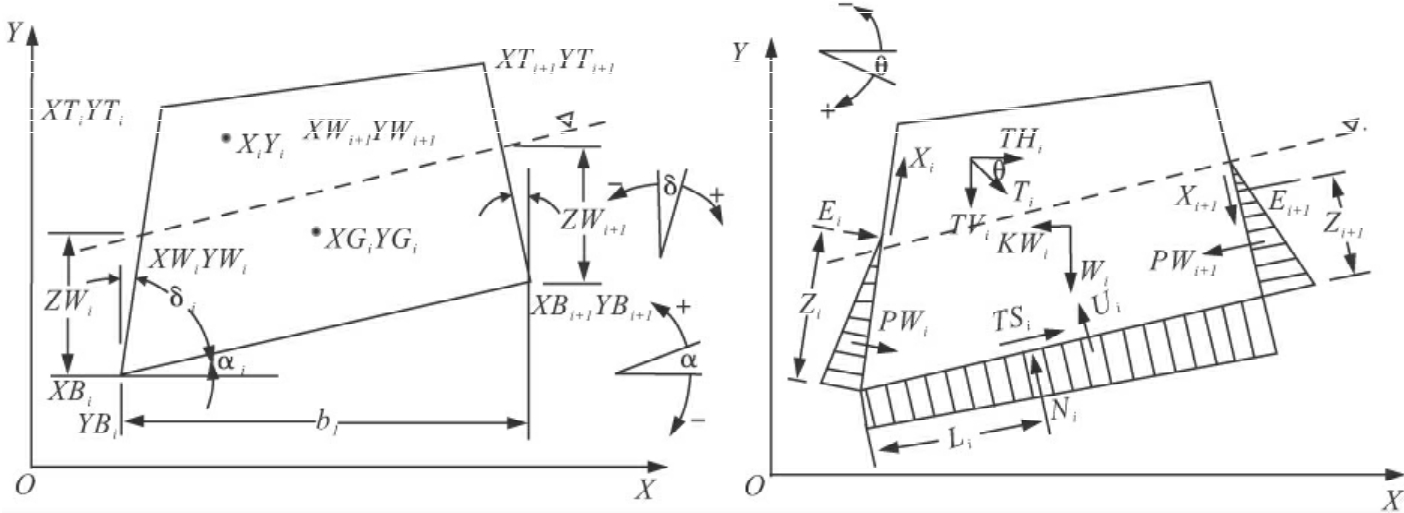
图8-8　第i块滑块几何形状和受力特征

式中:AE＝a_n＋a_n-1e_n＋a_n-2e_ne_n-1＋…a₁e_ne_n-1…e₃e₂

PE＝P_n＋P_n-1e_n＋P_n-2e_ne_n-1＋…P₁e_ne_n-1…e₃e₂

其中，a_i＝Q_i［Wi＋TV_isin（φbi-α_i）-THicos（φbi-α_i）＋R_icosφbi＋S_i＋1sin（φbi-α_i-δ_i＋1）-S_isin（φbi-α_i-δ_i）］

P_i＝Q_iWicos（φbi-α_i）

e_i＝Q_i［cos（φbi-α_i＋φi-δ_i）/cosφsi］

Q_i＝cosφsi＋1/cos（φbi-α_i＋φsi＋1-δ_i＋1）

S_i＝C_sid_i-PWi·tanφs

S_i＋1＝C_si＋1d_i＋1-PWi＋1·tanφsi＋1

R_i＝C_bib_i/cosα_i-Uitanφbi

（i＝1，…，n）

式中:C_bi、φbi——条块底面黏聚力（kPa）和内摩擦角，°；

C_si、φsi、C_si＋1、φsi＋1——条块两侧粘聚力（kPa）和摩擦角，°。

按式（8-17）可以求解滑体处于极限平衡状态时的临界水平加速度。而静态稳定系数通过下列途径获得:取不同的稳定系数F_s值，迭代变更条块底面和侧面上的剪切强度值，即将C_bi/F_s、tanφbi/F_s、C_si/F_s、tanφsi/F_s代入式（8-17）直至K＝0，这样求得的F_s值即为所分析剖面的稳定系数，但必须满足每个条块上的有效正应力为正值时，才是可接受的。

将上述有关参数输入Sarma法计算程序，即可求得计算剖面各滑动面所构成的滑体在某受力条件下的稳定系数F_s。