地震勘探：直达波、折射波、反射波及应用实例

4.4.3　地震勘探

地震勘探是通过人工激发的弹性波在地下传播的特点来解释判断某一地质体问题。由于岩（土）体的弹性性质不同，弹性波在其中的传播速度也有差异，利用这种差异可判定地层岩性、地质构造等。按弹性波的传播方式，地震勘探主要分为直达波法、折射波法、反射波法。

1.直达波法

由震源直接（不经过地质体界面的反射和折射）传播到接收点的波称直达波。利用直达波时距曲线（弹性波到达观测点的时间t和到达观测点所经过的距离S的关系曲线）可求得直达

波速，从而解决某些勘探问题。

直达波时距曲线为直线，其表达式如下:

式中:t——直达波从震源到达接收点的时间，s；

S——直达波从震源到达接收点的直线距离，m；

v——直达波的波速。根据其外业工作性质、条件不同，可分纵波波速v_p和横波波速v_s，m/s。

直达波法具有勘探和原位测试双重功能。广泛应用的波速测试实际就是直达波法的进一步应用。

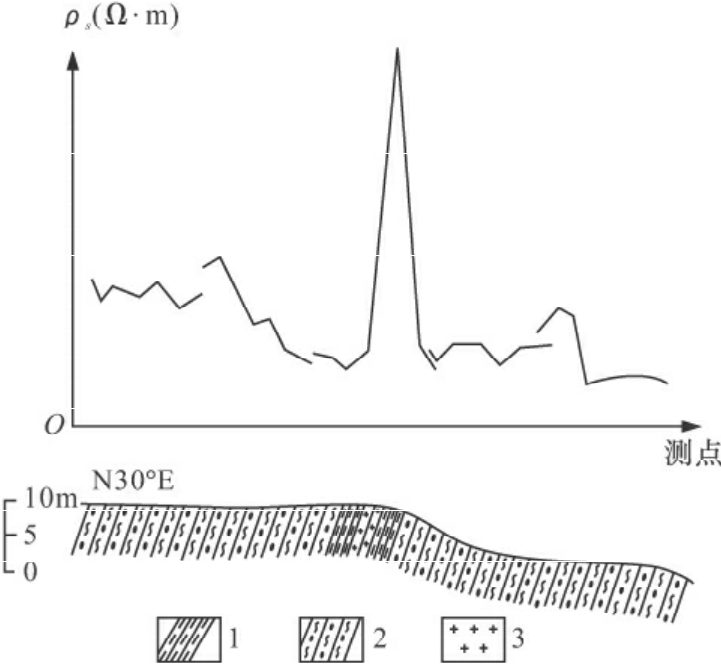
图4-26　用中间梯度法追索伟晶岩脉的ρs曲线

1-伟晶岩脉；2-矽线石、石榴子石片麻岩；3-黑云母片麻岩

2.折射波法

弹性波从震源向地层中传播，若遇到性质不同的地层界面时，就会遵循折射定律发生折射现象（图4-27）。

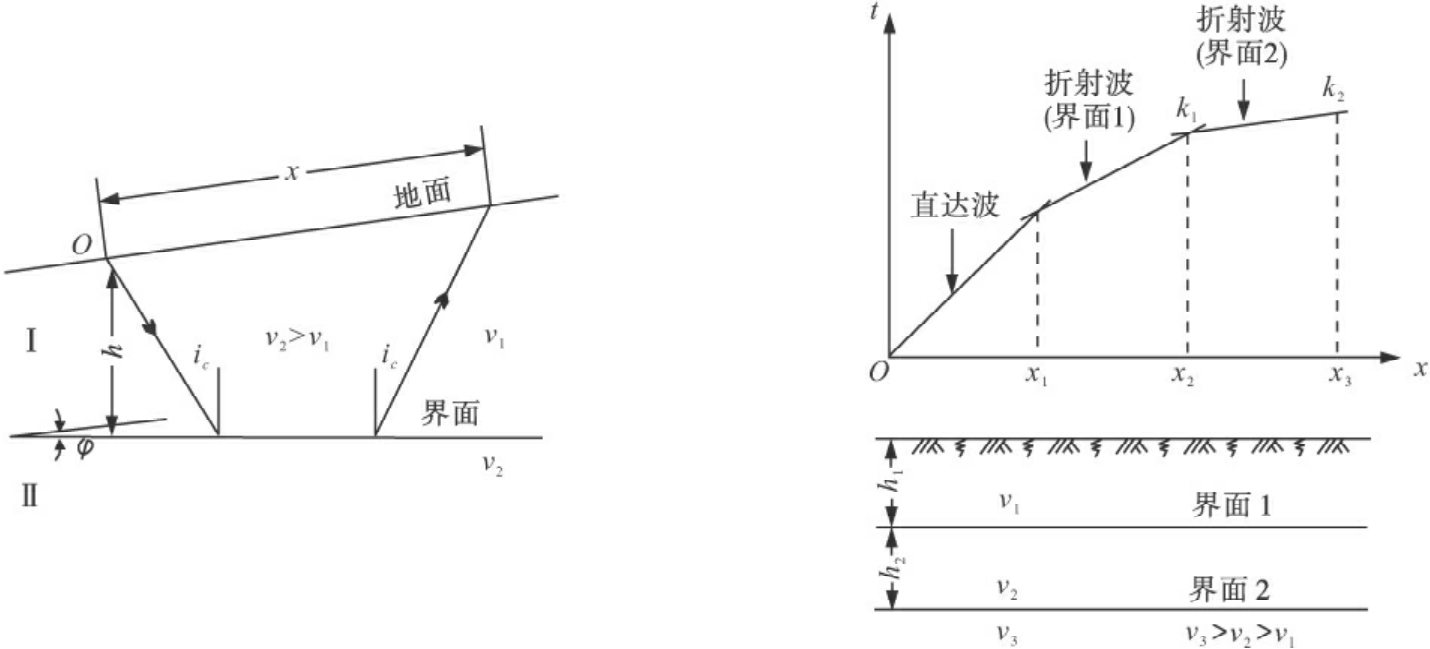
图4-27　折射波行程示意图　　　　　　　　图4-28　折射波时距曲线图

折射波的时距曲线表达式为:

式中:x——震源至观测点间的距离，m；

h——震源至折射界面的垂直距离（法线深度），m；(www.xing528.com)

v₁——上层介质（入射波）的波速，m/s；

v₂——下层介质（滑行波）的波速，m/s；

i——临界入射角（sini＝），°；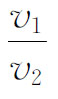

φ——平整界面的倾角，°。

当界面水平时，折射波时距曲线表达式则为

此时，折射波时距曲线如图4-28所示。

当地表下有n层水平界面时，折射波法的时距曲线方程为:

式中:t_n——第n层折射界面折射波到达观测点的时间，s；

x——震源至观测点间的距离，m；

h_k——第k层的厚度，m；

v_n——第n折射层的波速，m/s；

v_k-第k层中的波速，m/s；

i_n·k——在k层中折射波射线的临界入射角，°。

折射波在工程勘察中，是一种研究岩层界面（如基岩埋藏深度）、断层位置等的行之有效的方法。它的适用范围是:①界面以下波速必须大于界面以上波速，对三层或多层界面的情况，需各层波速递次增大，即v₁＜v₂＜…＜v_n；②界面无明显起伏，界面倾角φ需满足:i＋φ＜90°。

3.反射波法

弹性波从震源向地层中传播，遇到性质不同的地层界面时，遵循反射定律而发生反射。

反射波回到地面所需的时间与界面的深度有关。如果测得反射波到达地面所需的时间，做出反射波时距曲线，就可以推出所需探测的地层界面深度。

如图4-29为用浅层高分辨率地震勘探技术查明西安地裂缝带下隐伏的第四系断层的一个地震剖面。从图上不难看出，在断层两侧的t₁～t₆标准反射层均发生错断，断层上盘一侧的反射层深度加深，而断层下盘一侧的反射层深度相对变浅。而且随着反射层由t₁～t₆深度逐渐加深，各反射层所对应的断距逐渐加大，分析认为，此第四系断层是从基底（或下部）的断层不断继承性向上伸展的结果，这为西安地裂缝成因机制研究提供了重要信息。

图4-29　西安某地裂缝带下第四系断层的局部地震剖面解释图