8.3.7 控制图
8.3.7.1 概念
生产过程连续进行,在某一工序中加工出来的半成品或成品,其质量特性值可绘制成直方图,用来反映该工序在一定时间内的质量情况以及判断工序能力能否满足加工需要,但这仅能反映一定时间内生产过程的情况。即使当工序能力能满足加工质量的要求,也由于生产过程中影响质量的各种因素在一定范围内会有变化,工序能力也会随着时间的推移有所波动,从而使产品质量随之波动。因此,为了能及时掌握并控制工序质量随时间的动态变化,常需要借助于控制图。
控制图,也称为管理图,是用来分析和判断过程是否处于稳定状态并带有控制界限的图形。它是1924年由美国休哈特博士首先提出来的,因此也称休哈特控制图。控制图可以展示生产过程中质量随时间的变动情况,能及时发现异常、采取措施,从而对生产过程进行质量管理。由于控制图把产品质量控制从事后检验变为事前预防,为保证产品质量、降低生产成本、提高生产率开辟了广阔前景,因此在生产过程管理中得到了广泛应用。现在,控制图已成为实施质量管理时的常用工具。我国已制定了有关控制图的国家标准,即GB/T4091-2001,称为常规控制图。
8.3.7.2 控制图的基本形式
控制图的基本形式如图8.12所示。横坐标表示取样时间或样本序号;纵坐标表示质量特性值;上、下两条虚线分别表示上控制界限(UCL,Upper Control Limit)和下控制界限(LCL,Lower Control Limit);中间的实线表示中心线(CL,Central Line)。
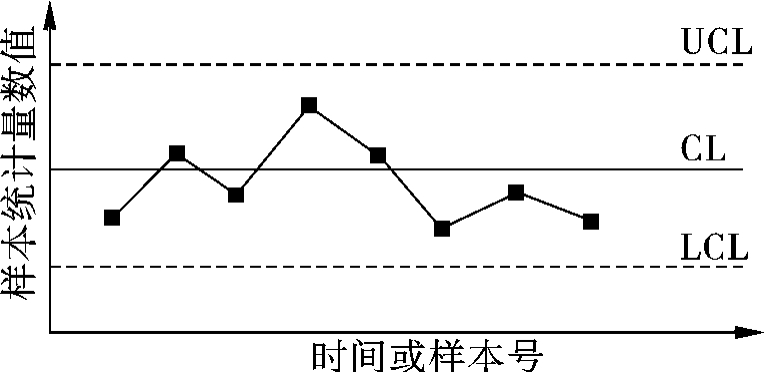
图8.12 控制图
在生产过程中,控制图的坐标系及三条控制线是由质量管理人员事先经过工序能力调查及其数据的收集与计算绘制好的。工序的操作人员按预先规定好的时间间隔抽取规定数量的样品,测得其质量特性值用点子描在控制图上相应位置即得到控制图,并通过点子的位置及排列情况判断工序状态。如果点子全部落在上下控制界限之内,且点子的排列无缺陷(参见后面“控制图的判断规则”部分),则判断生产过程处于稳定状态。如果点子越出上下控制界限,或点子排列有缺陷,则认为生产过程中存在异常因素,过程处于非稳定状态。这时就要查明原因,采取措施,使生产过程恢复正常。
8.3.7.3 控制图的原理
(1)正态性假定 任何生产过程,生产出来的产品,其质量特性值总会存在一定的波动,即正常波动和异常波动。当生产过程中只有偶然性因素时,虽然产品的质量特性值仍存在偏差,但这种偏差是稳定的,而且有一定的分布规律,不随时间而变化。总体不随时间变化的生产状态称为稳定状态或受控状态。此时,绝大多数质量特性值均服从或近似服从正态分布,这一假定称为正态性假定。控制图的作用就在于能判断生产过程是否处于稳定状态,即判断生产过程中是否存在系统性因素在起作用。
(2)控制界限的确定原理(3σ原理) 对于偶然性因素和系统性因素引起的质量波动,过去人们是直接凭经验进行判断和区别的。发明了控制图之后,就可以使用控制图对工序状态进行客观的、科学的判断。而区别和判断两类因素造成的质量波动的标准就是控制界限。因此,如何合理地、经济地确定控制界限是控制图的核心问题。
休哈特控制图控制界限是以3σ原理确定的,即以质量特性统计量的均值μ作为控制中线CL,在距均值±3σ处作控制上、下线。由3σ原理确定的控制图可以在最经济的条件下达到保证生产过程稳定的目的。
当生产过程中仅有偶然性因素存在时,质量特性值X服从正态分布N(μ,σ2),则根据正态分布的概率性质,有
P{μ-3σ<X<μ+3σ}=99.73% (8.17)
即从过程中测得的质量特性值X有99.73%落在μ±3σ的范围内,落在μ±3σ的范围外的概率只有0.27%。按照小概率事件原理,在一次实践中超出μ±3σ范围的小概率事件一般是不会发生的。如果发生了,则认为过程中存在系统性因素在起作用,生产过程处于失控状态。这就是休哈特的3σ原理。
根据此原理,控制界限的一般公式为
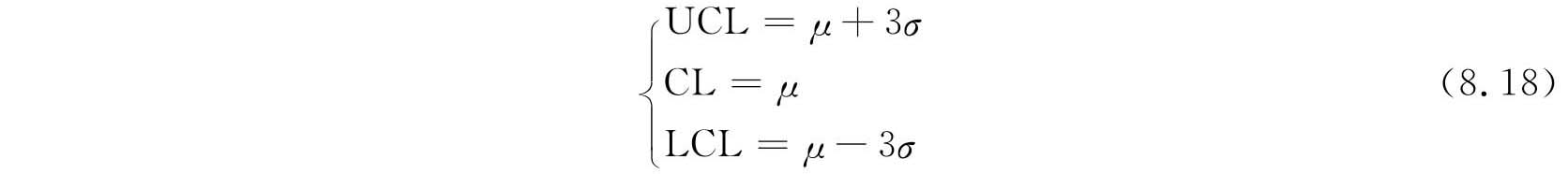
(3)两类错误 利用控制图来判断生产过程是否稳定,实际上是一种统计推断的方法,因而可能会产生两类错误。
1)第一类错误是将正常判为异常,即在生产正常的情况下,只是由于偶然性因素的影响而使点子超出界限,而我们却把它判为存在系统性因素造成过程异常,从而犯虚发警报的错误,发生这种错误的概率通常记为α,见图8.13。
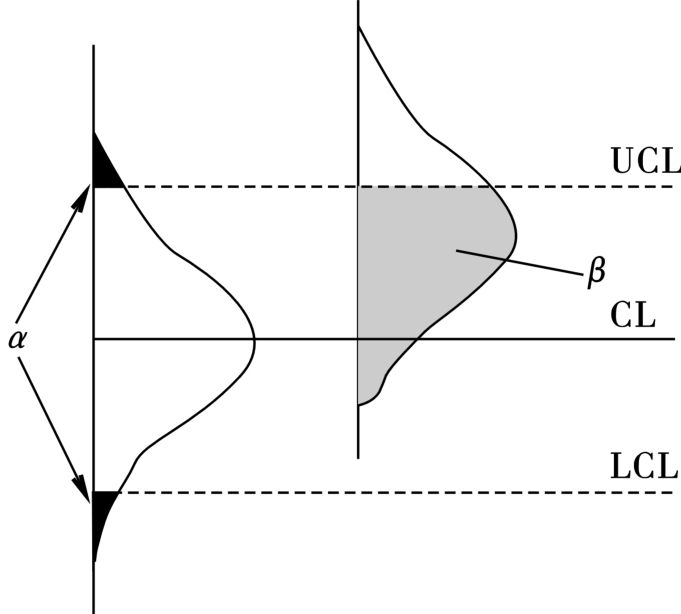
图8.13 两类错误及其发生概率示意图
2)第二类错误是将异常判为正常,即生产过程已经存在系统性因素的影响,但因某种原因,质量特性值并没有越出控制界限。如果抽到这样的产品进行检测,则会由于点子未出界而判断生产正常,从而犯漏发警报的错误,其发生的概率通常记为β,见图8.13。
孤立地看,哪一类错误都可以避免:放宽控制界限,即控制界限系数k越大,第1类错误的概率α越小,第2类错误的概率β越大;反之,加严控制界限,即控制界限系数k越小,第1类错误的概率α越大,第2类错误的概率β减小。但要同时避免两类错误却是不可能的,因为减少第1种错误就会增加第2种错误;反之,减少了第2种错误,就会增加第一种错误。那么,怎么确定一个合理的控制界限而使两类错误的造成的合计损失为最小呢?两类错误损失相加为最小的地方,就应是控制界限所在之处,即控制界限系数k的确定应以两类错误判断的总损失最小为原则。经验证明,当k=3时,即控制图上下界限距中心线CL为±3σ时,合计损失为最小。
8.3.7.4 控制图的种类
(1)按产品质量特性的不同,控制图分为计量值控制图与计数值控制图两大类
1)计量值控制图 适用于产品质量特性为计量值的情形,如长度、质量、时间等连续变量。常用的计量值控制图有:单值-移动极差控制图(x-Rs控制图)、均值-极差控制图(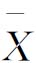 -R图)、均值-标准差控制图(
-R图)、均值-标准差控制图(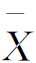 -S图)以及中位数-极差控制图(
-S图)以及中位数-极差控制图(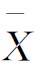 -R图)。
-R图)。
其中x-Rs控制图是计量值最基本的控制图,其中移动极差Rs是指相邻的两个观测值之差的绝对值,即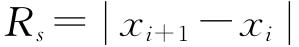 ,它是利用单个样品的质量特性数据直接对生产进行控制,不需要繁琐计算,使用方便,具有直接发现异常的特点。x-Rs控制图适用于取样费时、费用高、破坏性或样品性质均匀等场合,如日耗电量、破坏性测试等。但x-Rs控制图不够敏感,不易发现工序质量平均值的变化,不大适用于大规模快速生产的需要。
,它是利用单个样品的质量特性数据直接对生产进行控制,不需要繁琐计算,使用方便,具有直接发现异常的特点。x-Rs控制图适用于取样费时、费用高、破坏性或样品性质均匀等场合,如日耗电量、破坏性测试等。但x-Rs控制图不够敏感,不易发现工序质量平均值的变化,不大适用于大规模快速生产的需要。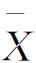 -R控制图是连续型变量最常用的控制图,其中
-R控制图是连续型变量最常用的控制图,其中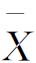 为样本平均数,R为极差,它对加工工序有很强的控制能力,可避免x-Rs控制图易受个别极端值的影响而犯第一类错误,比x-Rs控制图的敏感性强,是控制产品质量最实用有效的一种工具。
为样本平均数,R为极差,它对加工工序有很强的控制能力,可避免x-Rs控制图易受个别极端值的影响而犯第一类错误,比x-Rs控制图的敏感性强,是控制产品质量最实用有效的一种工具。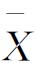 -S控制图比
-S控制图比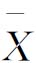 -R控制图能更精确的反映工序的变化,但计算工作量大。
-R控制图能更精确的反映工序的变化,但计算工作量大。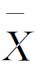 -R控制图的优点是可以减少计算,受异常数据影响小,但检出力不如
-R控制图的优点是可以减少计算,受异常数据影响小,但检出力不如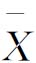 -R控制图高。
-R控制图高。
2)计数值控制图 适用于产品质量特性为计数值的情形,如不合格品数、不合格品率、缺陷数等离散变量。这类控制图有不合格品数控制图(pn图)、不合格品率控制图(p图)、缺陷数控制图(c图)、单位缺陷数控制图(u图),其中不合格品数控制图(pn图)和不合格品率控制图(p图)适用于计件值数据,缺陷数控制图(c图)和单位缺陷数控制图(u图)适用于计点值数据。
(2)按用途和应用场合不同,控制图又分为分析用控制图和控制(管理)用控制图
1)分析用控制图 分析用控制图是在对生产过程控制之初,对过程稳定与否未知的情况下,收集数据分析过程是否处于稳定状态。若经分析后,过程处于稳态且满足质量要求,则把分析用控制图转为控制用控制图;若经分析后,过程处于非稳定状态,则应查找过程失控的异常原因,并加以消除,去掉异常数据点,重新计算中心线和控制界限线;若异常数据点比例过大,则应改进生产过程,再次收集数据,计算中心线和控制界限线;若经分析后,过程虽然处于控制状态,但不满足质量要求,则应调整生产过程的有关因素,直到满足要求才能转为控制用控制图。
2)控制(管理)用控制图 控制(管理)用控制图由分析用控制图转化而成,它用于对生产过程进行连续监控,以保证过程保持在稳定状态。控制用控制图在使用一段时间后,应根据实际情况对中心线和控制界限进行修改。
8.3.7.5 控制图的判断准则
(1)控制图的设计思想 控制图的设计思想是先确定第1类错误的概率α,然后再根据第2类错误的概率β的大小来考虑是否需要采取必要的措施。通常为了增加使用者的信心,α都取得特别小,为0.27%~0.3%。所以,当控制图上的点子超出界限时,就可认为过程失控。但是α小,β就大。因此,为了减少第2类错误,对于控制图中的界内点又增添了第二条判异准则,即当控制界限内的点子排列不随机时,就认为过程失控。于是判断异常的准则就是两大类:①点子出界判断异常;②界内点排列不随机判断异常。
(2)判断稳态的准则 稳态是生产过程追求的目标,要在控制图上判断过程是否处于稳态,就需要制定判断稳态的准则。在统计量为正态分布的情况下,由于第1类错误的概率α=0.27%取得很小,所以只要有一个点子在界外就可以判断有异常。但既然α很小,第2类错误的概率β就大,故只根据一个点子在界内远不能判断生产过程处于稳态。如果连续有许多点子,如25个点子,全部都在控制界限内,根据概率乘法定理,β总=β25,要比单个点在界内的β减少很多。如果连续在控制界内的点子更多,则即使有个别点子出界,过程仍可看做是稳态,这就是判稳准则。
根据判稳准则,在点子随机排列的情况下,符合下列条件之一就可认为过程处于稳态:①连续25个点子都在控制界限内;②连续35个点子至多1个点子落在控制界限外;③连续100个点子至多2个点子落在控制界限外。这三个判定条件的可靠性依次递增,因为通过概率计算其α递减;另一方面,这三个判定条件的样品个数依次递增,成本逐次升高。因此在判断时应从①开始,若其不能判断,则进行②,若还不能就进行③。但由于①α较大,虚报较多,应尽量采用②和③。
(3)判断异常的准则 控制图上的点子未超出界限,但界内点排列不随机也认为过程失控。由于对点子的数目未加限制,故界内点子排列不随机的方式理论上可以有许多种,但现场能够保留下来继续使用的只有具有明显物理意义的若干种模式,分别为:
1)模式1 点子屡屡接近控制界限,如图8.14所示。所谓接近控制界限指点子距离控制界限在1σ以内。这时,属于下列情况之一的就判断点子排列不随机,存在异常因素:①连续3个点中,至少有2个点接近控制界限;②连续7个点中,至少有3个点接近控制界限;③连续10个点中,至少有4个点接近控制界限。
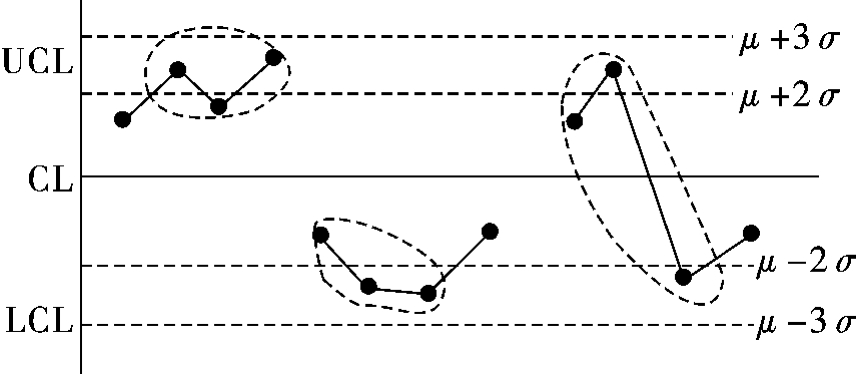
图8.14 连续3个点中有2个点接近控制界限
直观看来,若点子接近一侧的控制界限,表明过程的均值向这一侧偏移;若点子上下接近两侧的控制界限,则表明过程的方差增大。由于后两条准则需要观察的点子数较多,应用起来不方便,所以主要应用第一条准则。
2)模式2 链。在控制图中心线一侧连续出现的点称为链,其点子数目称作链长,如图8.15所示。链长不少于7时判断点子排列非随机,存在异常因素。直观看来,出现链表示过程均值向链这一侧偏移。如果链较长,那么即使个别点子出现在中心线的另一侧面而形成间断链,也可按照与链类似的方式处理。
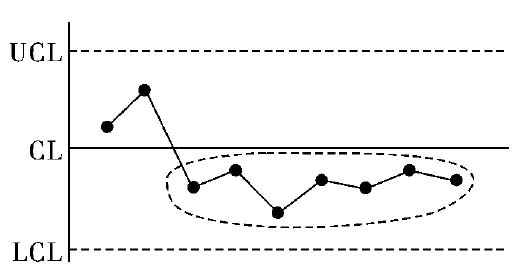
图8.15 长为7的链
3)模式3 间断链,如图8.16所示。属下列情况的就判断点子排列非随机,存在异常因素:①连续11个点中,至少有10个点在中心线一侧;②连续14个点中,至少有12个点在中心线一侧;③连续17个点中,至少有14个点在中心线一侧;④连续20个点中,至少有16个点在中心线一侧。
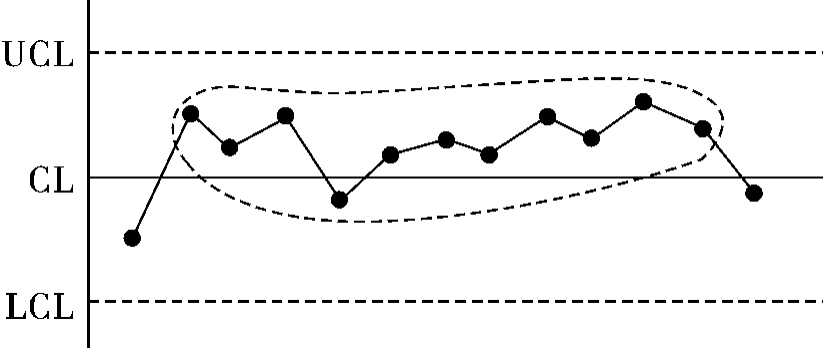
图8.16 连续11个点中有10个点在一侧
4)模式4 单调链。若干个点连续上升或下降时,这些点所连成的折线称为单调链,如图8.17所示。当有连续不少于7个点的上升或下降的趋向时就判断点子排列非随机,存在异常因素。直观看来,出现倾向表明过程均值逐渐增大或逐渐减少。
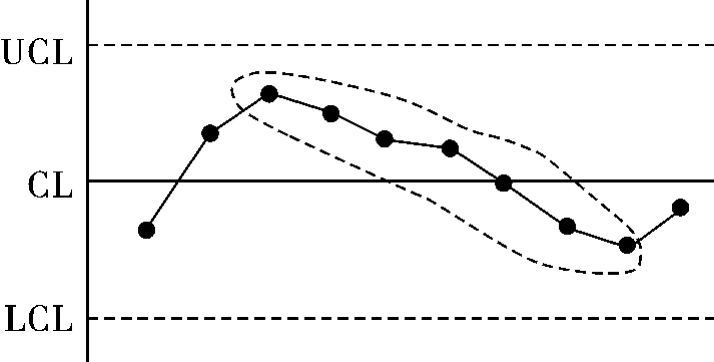
图8.17 7点下降趋向
5)模式5 点子集中在中心线附近。所谓中心线附近指点子距离中心线在1σ以内,如图8.18所示。出现这种情况表明过程方差异常小,但通常模式5可能因数据不真实或者数据分层不当这两个原因造成。对于后者,如果把方差大的数据与方差小的数据混合在一起而未分层,则混合数据的方差更大,于是控制图上下控制界限的间隔距离也将较大,这时如将方差小的数据描点就可以出现模式5的情况。
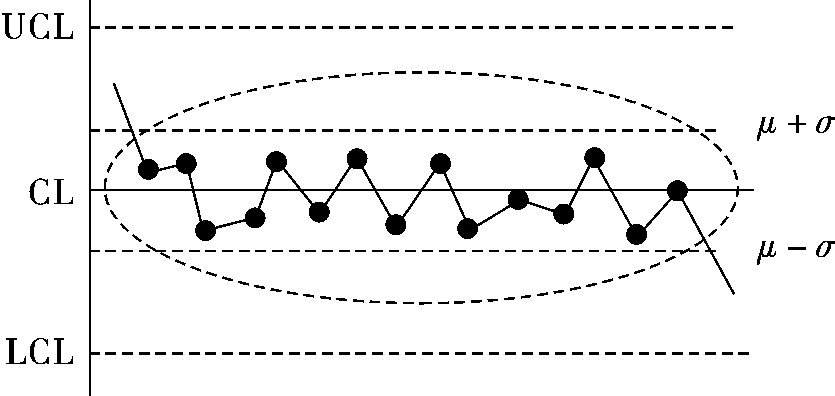
图8.18 连续16点集中在中心
6)模式6 点子呈现周期性变化,如图8.19所示。造成点子周期性变化的原因可能有:操作人员疲劳、原材料的发送有问题、某些化工过程热积累或某些机械设备应用过程中的应力积累等。消除上述周期性变化可以减少产品质量的波动,改进产品的质量。
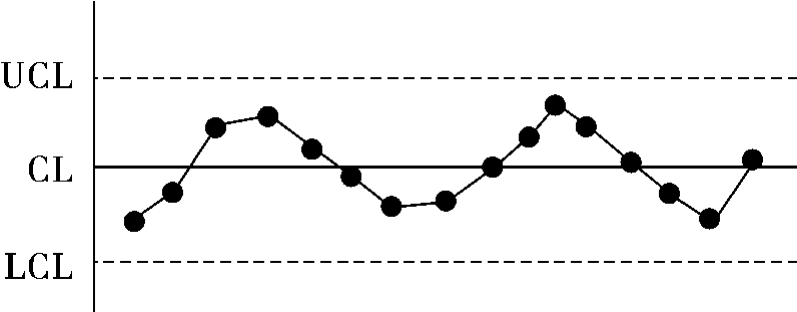
图8.19 点子呈周期性变化
8.3.7.6 控制图的应用
(1)控制图的应用程序
1)选定控制图 对于不同的控制项目或不同的质量特性,应选用不同类型的控制图。
2)收集数据作分析用控制图 必须采取近期生产中的数据,一般需20~25组数据,每组数据的多少由控制图种类及经济性来决定,根据收集的数据作分析用控制图。
3)稳定状态的判断 用分析用控制图判断生产过程是否处于稳定状态,若发现有异常,需针对异常找出原因,并将异常数据剔除,重新计算控制界限;或者重新收集数据。
4)判断生产过程是否能够满足规定的质量要求 若能够满足,则可将此时的分析用控制图转化为控制用控制图,否则应重新调整生产过程有关要素,直至生产过程能够满足规定的质量要求,方可将分析用控制图转化为控制用控制图。
5)利用控制用控制图对生产过程进行监控 在生产过程中取样,并将其结果在控制图上画点,判断生产过程所处状态,一旦发现生产过程处于非稳定状态,则要针对异常数据点查明原因,并加以消除。
6)修改控制图 控制图使用一段时间后,如出现下述情况之一,应重新计算中心线和控制界限:①大修或停产;②工况发生较大变化;③质量发生明显改进,原控制界限显得太宽已失去控制作用。
(2)控制图的应用实例
1)计量值控制图 以均值-极差控制图(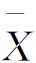 -R图)为例加以说明,它是一种常用的计量值控制图。
-R图)为例加以说明,它是一种常用的计量值控制图。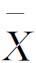 -R图是
-R图是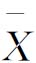 图(均值控制图)和R图(极差控制图)联合使用的一种控制图,
图(均值控制图)和R图(极差控制图)联合使用的一种控制图,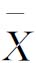 图主要用于判断生产过程的均值是否处于或保持在所要求的受控状态,
图主要用于判断生产过程的均值是否处于或保持在所要求的受控状态,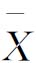 图比单值(x)控制图发现异常的敏感能力强;R图用于判断生产过程的标准差是否处于或保持在所要求的受控状态。
图比单值(x)控制图发现异常的敏感能力强;R图用于判断生产过程的标准差是否处于或保持在所要求的受控状态。
【例8.5】 某厂生产一种零件,其长度要求为49.50mm±0.10mm,生产过程质量要求为过程能力指数不小于1,为对该过程实施连续监控,试设计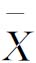 -R图。
-R图。
解:①收集数据并加以分组
在5M1E充分固定,且标准化的情况下,从生产过程中收集数据。通常,每组样本大小n≤10,组数k≥25。
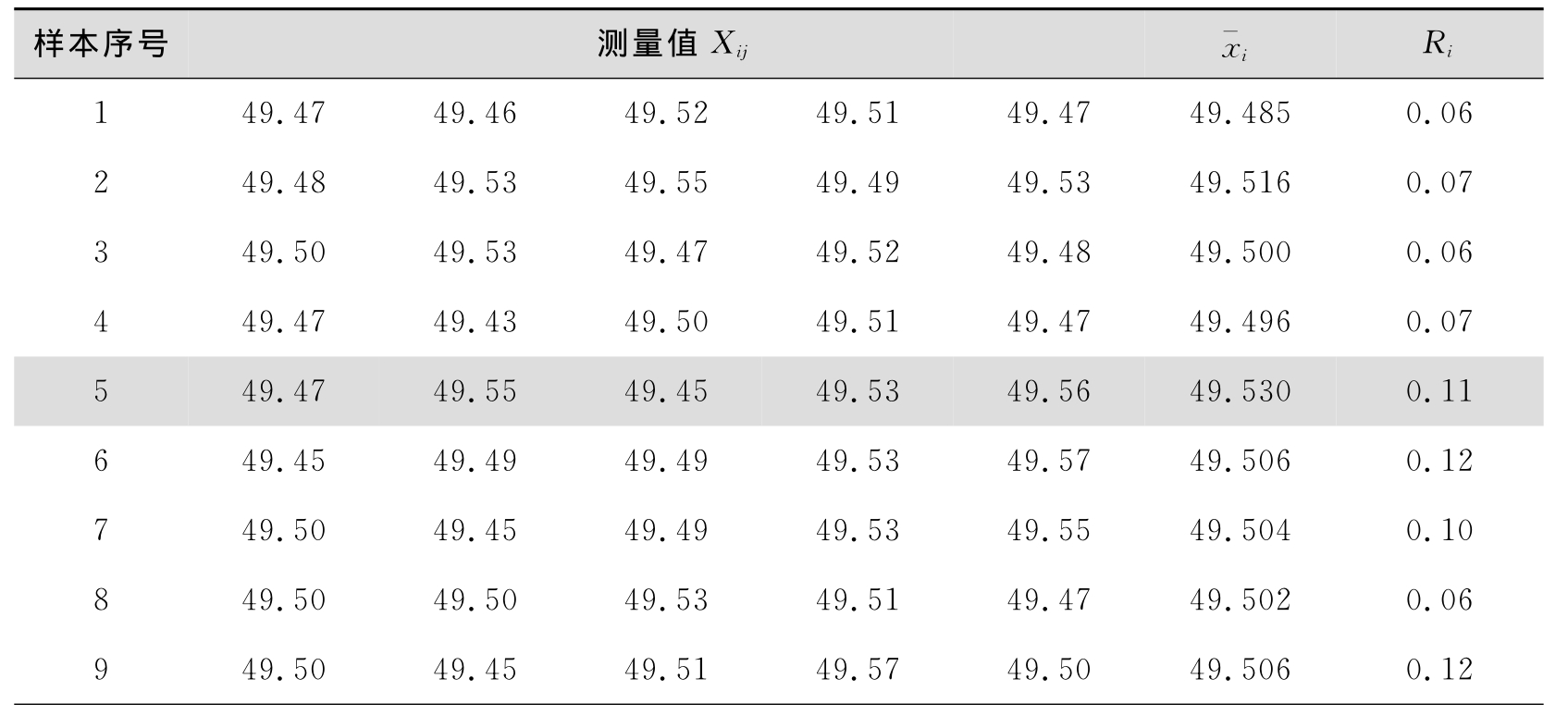
本例一共收集25个样本,每个样本包含5个零件长度的测量值,数据如表8.14所示。
表8.14 某零件长度值的数据表/mm
 (https://www.xing528.com)
(https://www.xing528.com)
续表8.14
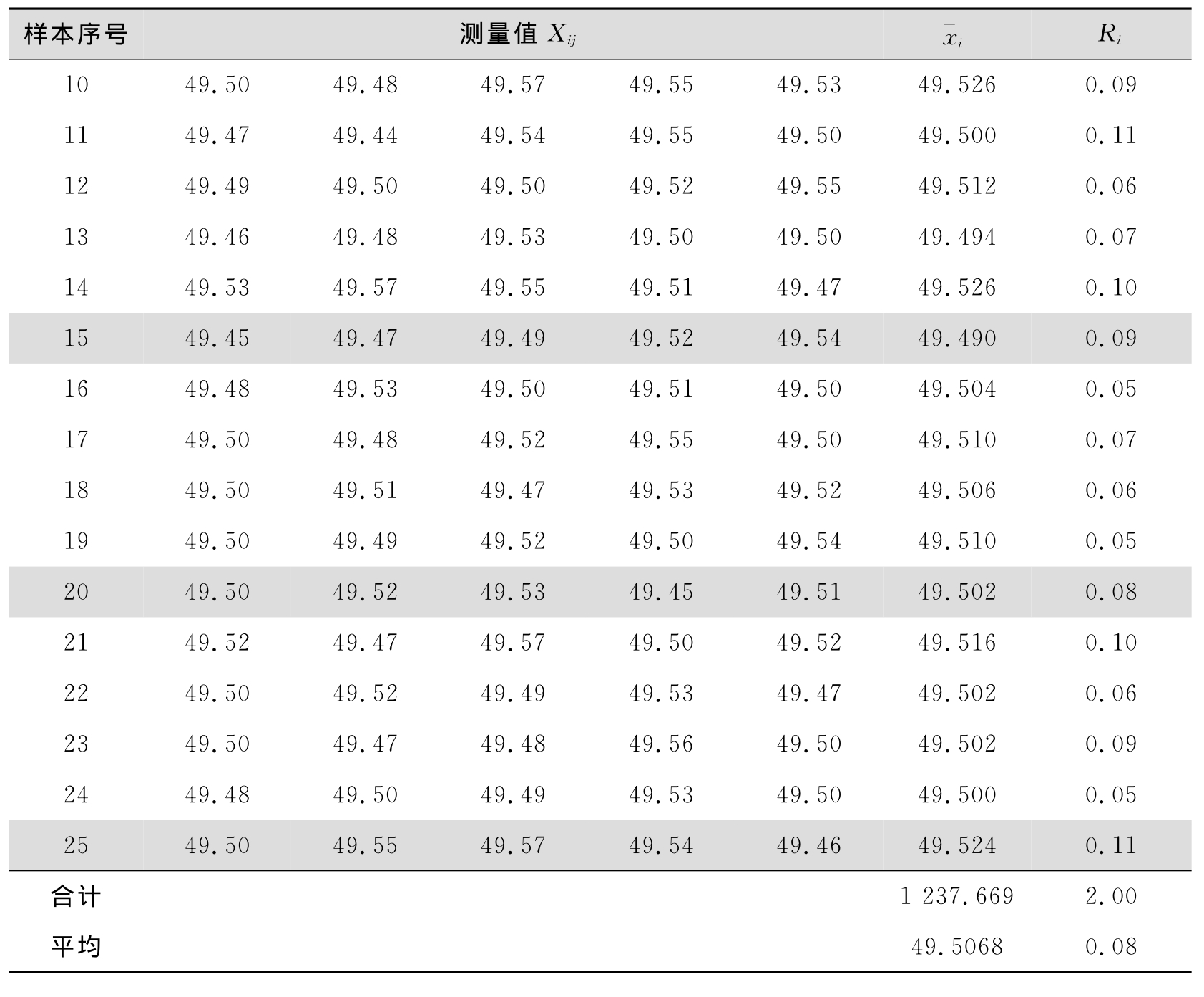
②计算每组的样本均值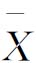 和样本极差R
和样本极差R
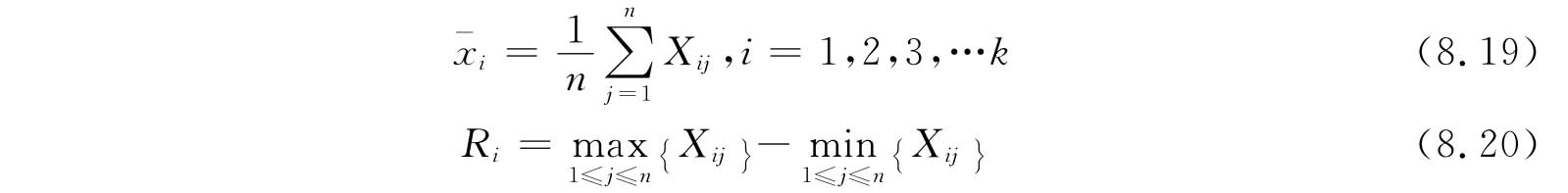
本例中n=5,k=25,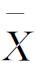 i、Ri的计算结果如表8.14所示。
i、Ri的计算结果如表8.14所示。
③计算样本总平均值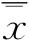 和平均样本极差R-
和平均样本极差R-
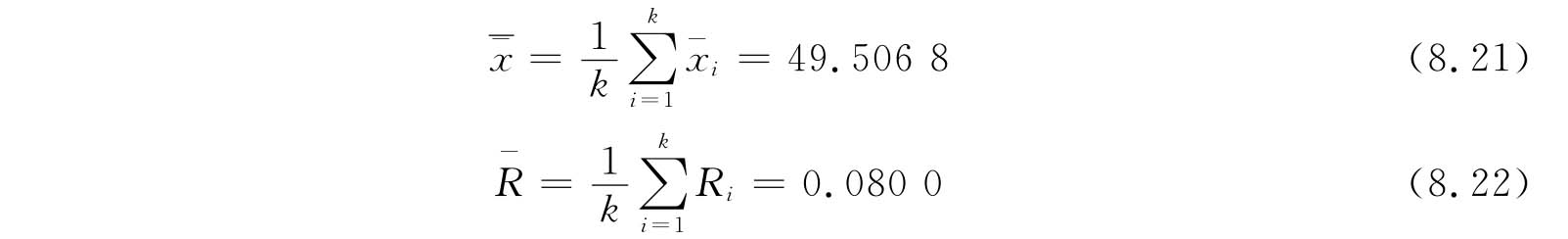
④计算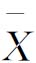 图和R图的控制线
图和R图的控制线
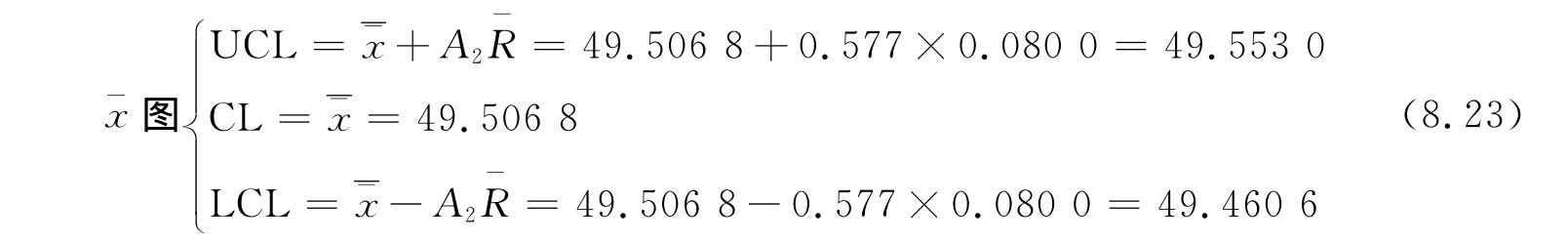
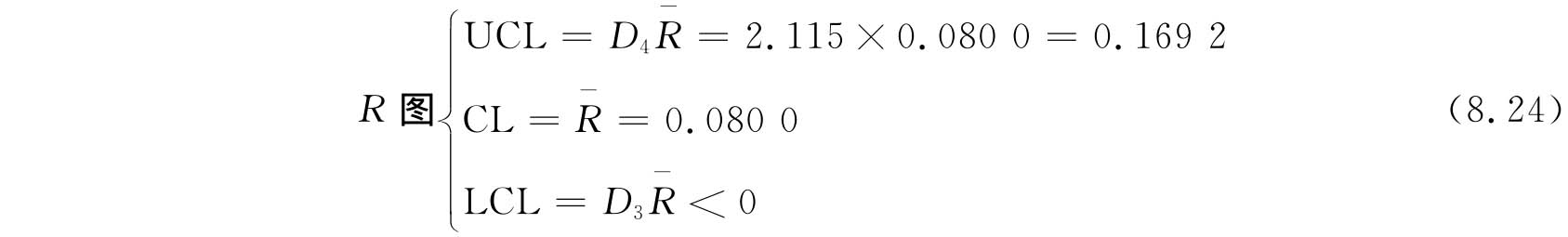
式中 A2、D4、D3均是由n确定的系数,从控制图系数表中可查得:当n=5时,A2=0.577,D4=2.115,D3<0。
⑤画控制图
分别作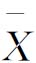 图和R图,两张图必须画在同一页纸上,以便对照分析。
图和R图,两张图必须画在同一页纸上,以便对照分析。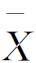 图在上,R图在下,纵轴在同一直线上,横轴相互平行,并且刻度对齐。中心线用实线表示,控制接线用虚线表示。本例由于R图的下限为负值,但极差R不可能为负值,所以R图的下控制界限不存在。然后在各控制界限的右方记入相应的符号和数值,并根据各样本的
图在上,R图在下,纵轴在同一直线上,横轴相互平行,并且刻度对齐。中心线用实线表示,控制接线用虚线表示。本例由于R图的下限为负值,但极差R不可能为负值,所以R图的下控制界限不存在。然后在各控制界限的右方记入相应的符号和数值,并根据各样本的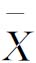 i值和Ri值在控制图上描点,见图8.20。
i值和Ri值在控制图上描点,见图8.20。
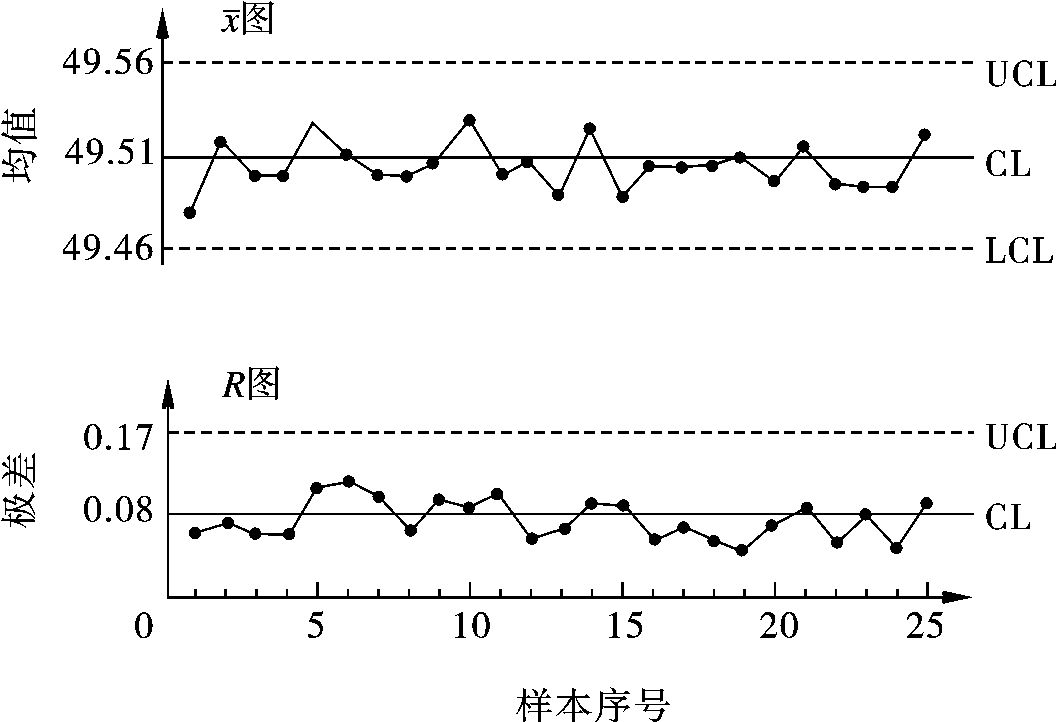
图8.20 零件长度的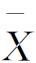 -R图
-R图
⑥分析过程是否处于稳定状态
根据控制图的判断准则,分析过程是否处于稳定状态。经分析知本例的生产过程处于稳定状态。
⑦判断过程是否能够满足规定的质量要求
计算生产过程实际的工序能力指数,并与规定应满足的工序能力指数进行比较,从而判断过程是否满足规定的质量要求。
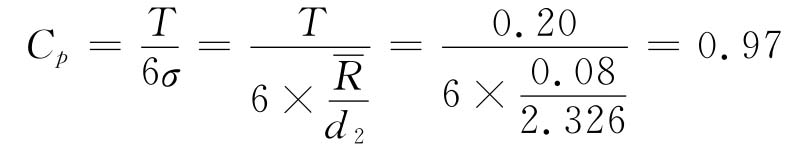
式中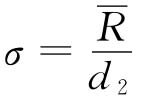 ,d2是由n决定的系数,查控制图系数表得:当n=5时,d2=2.326。
,d2是由n决定的系数,查控制图系数表得:当n=5时,d2=2.326。
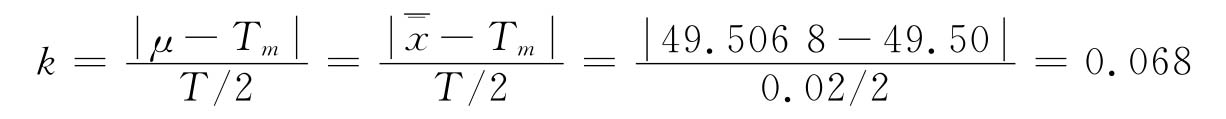
Cpk=(1-k)Cp=(1-0.068)×0.97=0.90<1
经计算,本例工序能力指数小于1,说明此过程不满足要求,所以不能将分析用控制图转化为控制用控制图,而是应采取措施,提高加工精度。
2)计数值控制图 以不合格品率控制图(P图)为例加以说明。P图用于判断生产过程不合格品率是否处于或保持在所要求的受控状态。P图适用于样本大小相等和不相等的情况,当应用于样本大小不相等的情况时,控制图的上、下控制界限往往不是一条直线,而是阶梯式的。
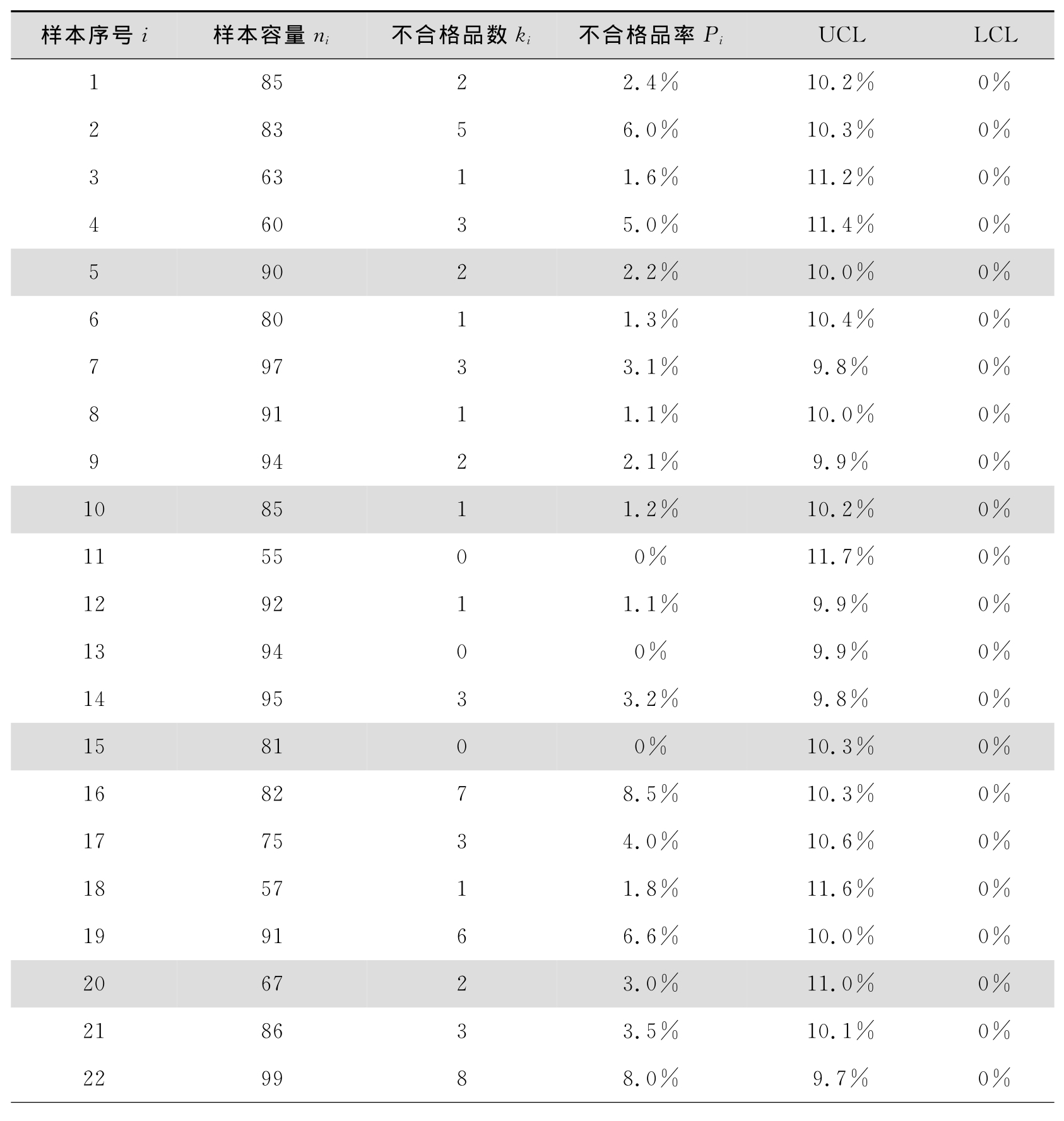
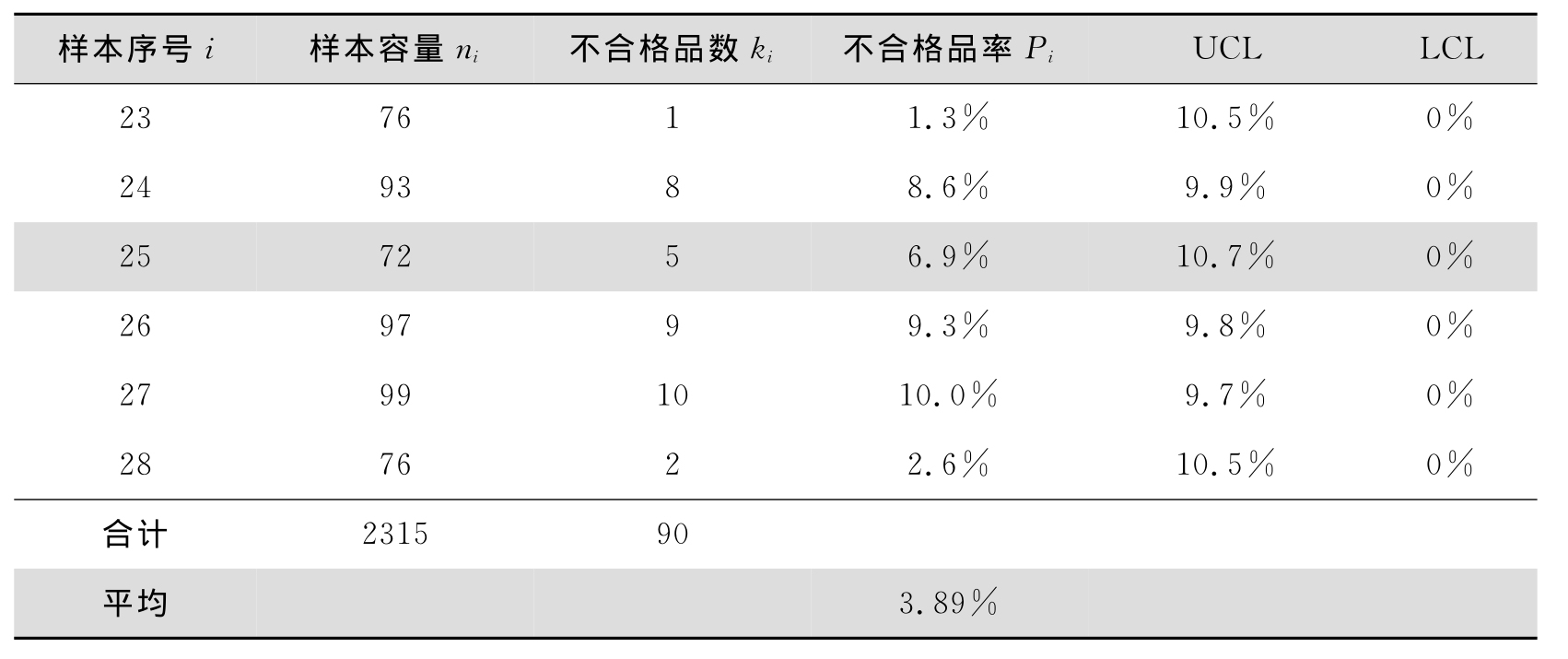
【例8.6】 某食品企业1月份产品质量检测结果如表8.15所示,试设计P图。
表8.15 某食品企业产品质量检测结果
续表8.15
解:①收集数据
本例已给定数据如表8.15所示,其样本大小各不相同。
②计算每组样本的不合格品率Pi
Pi=ki/ni, i=1,2,…k(8.25)
本例中k=28,pi的计算结果见表8.16。
表8.16 常见控制图控制界限的计算公式

续表8.16

③计算过程平均不合格品率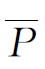
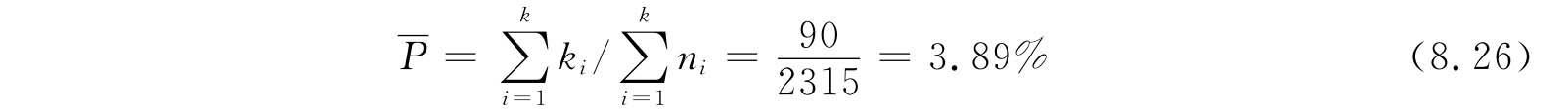
④计算控制线
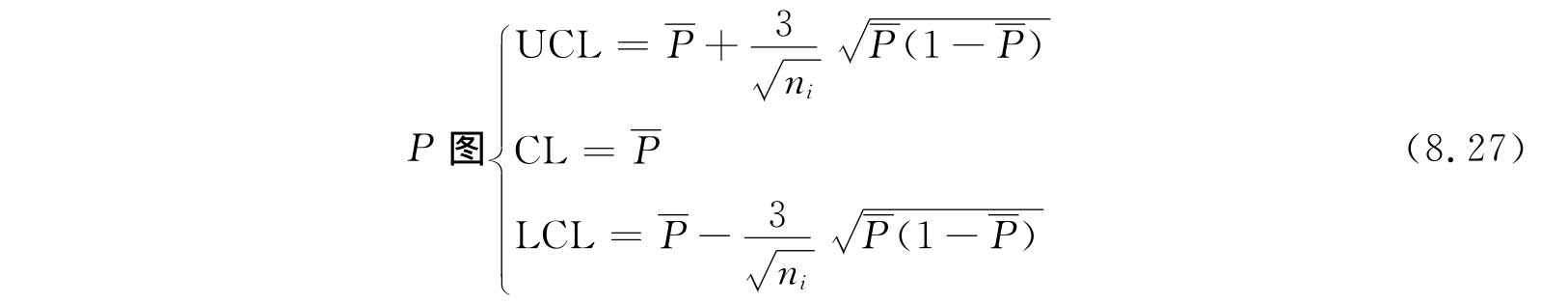
由于本例中每个样本的容量ni不相等,所以必须对每个样本分别求出其控制界限。如对于第一个样本,代入相应数值得
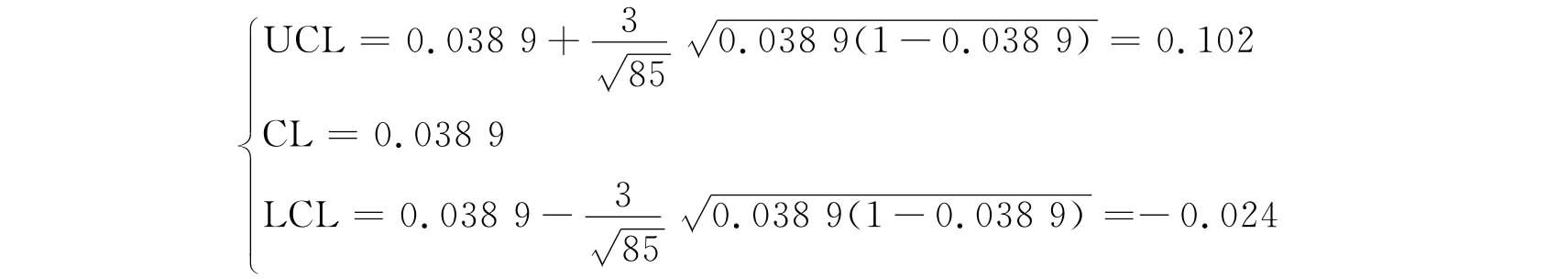
这里LCL取负值,但P不可能为负,故令LCL=0作为P1的自然下界。其余各个样本依此类推,结果见表8.16。
⑤画控制图
以样本序号i为横坐标,样本不合格品率Pi为纵坐标作P图,并根据每个样本的不合格品率Pi在控制图上描点,见图8.21。
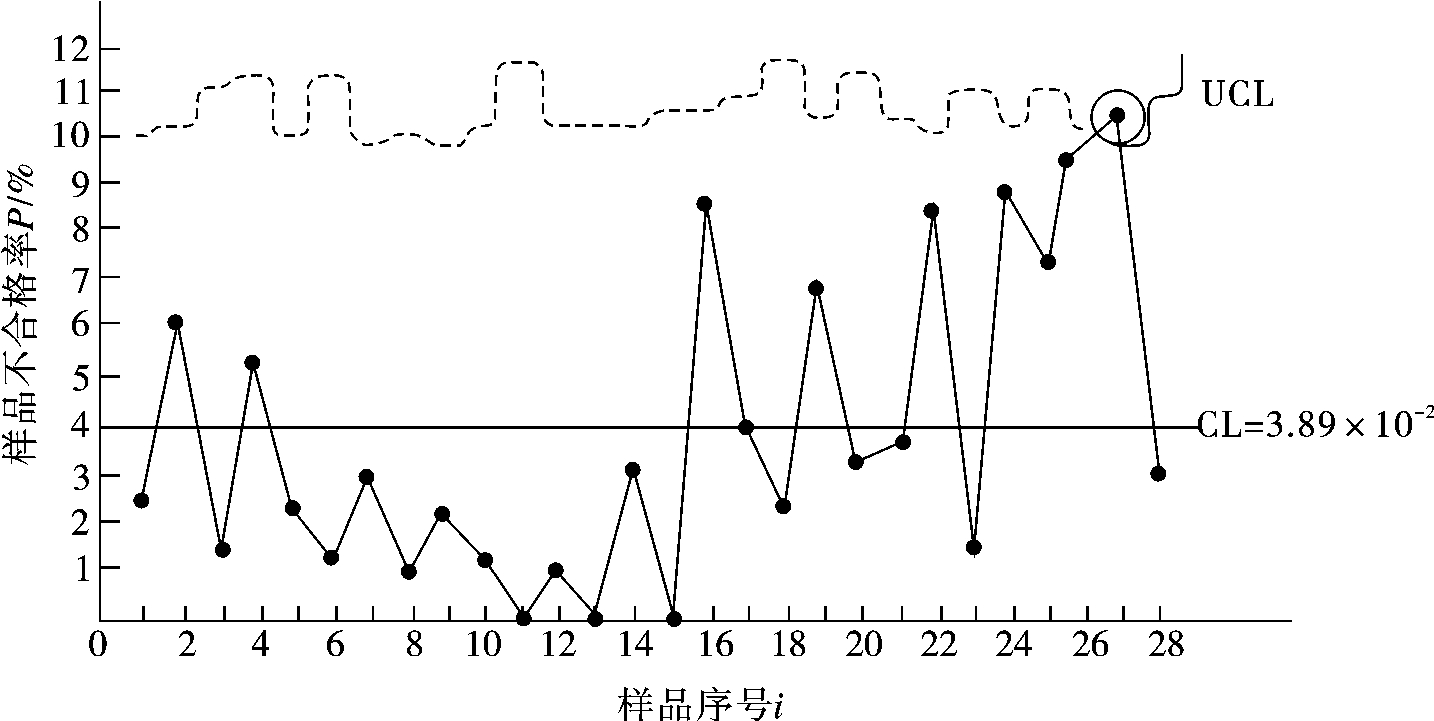
图8.21 某产品不合格品率的P图
⑥分析过程是否处于控制状态
从图8.21看出,第27个样本的点子出界,应查找异常的原因,加以纠正。但由于上控制界限凹凸起伏,不便于观察变差可查明原因的8种模式。实际中,对于各组样本大小不同的情况,国家标准GB/T 4091—2001《常规控制图》提出了两种解决方案。
方案一:如果样本大小差别不大,则可以采用平均样本大小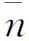 来代替各样本组的样本数ni,然后用
来代替各样本组的样本数ni,然后用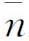 计算上下控制界限。通常当样本大小的变化在样本大小目标值的±25%之内时,采用此方案。
计算上下控制界限。通常当样本大小的变化在样本大小目标值的±25%之内时,采用此方案。
本例平均样本大小为:
![]()
而nmax=99,nmin=55,则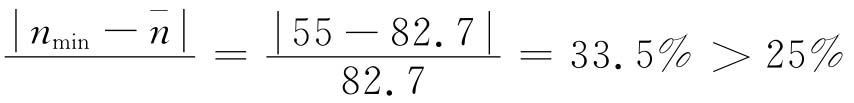 ,故本例不适合采用方案一的方法。
,故本例不适合采用方案一的方法。
方案二:当样本变化较大时,可采用利用标准化变量的方法。即不点绘P值,而改为点绘标准化值Z。标准化值Z的计算方法如下:
若已给定P的标准值P0,则
![]()
若没有给定P的标准值P0,则
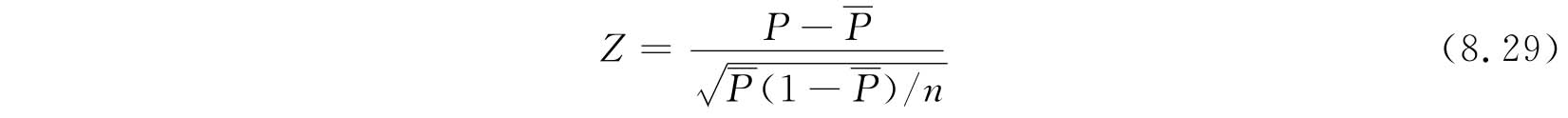
此时,标准化值Z的平均值和标准差分别为0和1,控制图的中心线和控制界限成为常数,与样本大小无关,由此得到通用控制图如下:
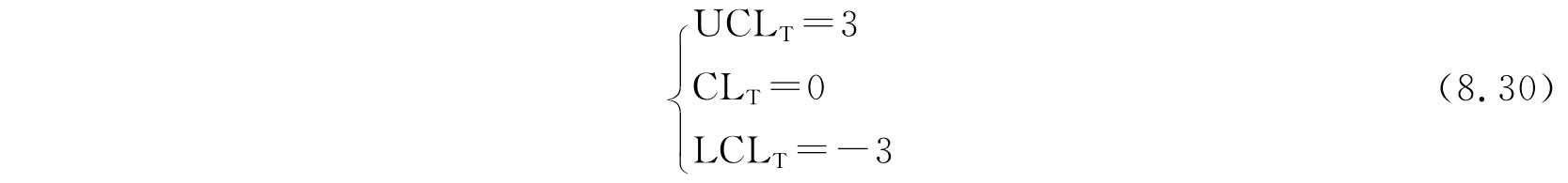
式中 下标“T”表示通用的“通”。由此通用控制图即可对样本变化较大的质量特性值作控制图,然后就可根据控制图的判断准则进行判断。
8.3.7.7 控制界限计算公式小结
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




