散布图的观察与分析：判断变量相关关系

8.3.6　散布图

8.3.6.1　概念

当分析、研究两个有关系的变量之间的问题时，常会发现存在两种不同的关系：一类是确定性的关系；一类是不确定性的关系。确定性的关系是指两个变量之间存在完全确定的函数关系，这种关系可以用确定的函数式来表达。例如做匀速直线运动的物体，速度v、时间t和走过的距离s之间存在着完全确定的函数关系s＝vt，其中任何一个变量一定时，另外两个变量之间的关系就确定。不确定性的关系是指两个变量之间虽然存在一定的相关关系，但是不能用确定的函数关系来表示，也就是说在不确定性的关系中两个变量之间是一种依赖和制约的关系，但不是一种必然的关系。例如儿童的体质量和儿童的年龄这两个变量之间的关系，一般来说儿童的体质量是随着年龄的增长逐渐增加的，但是儿童年龄的增长并不一定就会引起体质量的增加，儿童体质量的增加还受其他因素如遗传、营养状况、生活习惯等多种因素的影响，这些因素的综合作用都可能会造成儿童的体质量和年龄这两个变量之间的关系的不确定。

我们把这种不确定性的关系称为相关关系。散布图就是用来研究、判断两个变量之间相关关系的图，又称为散点图或相关图。它是将一对不确定性关系的变量用对应的点子表现在坐标图上来观察他们之间的关系。两个变量之间可能是特性－要因、特性－特性或要因－要因的关系。这种关系可进一步用相关系数做定量分析，也可作成回归直线控制图用于质量控制。

8.3.6.2　散布图的做法

散布图的做法就是把由实验或观测得到的统计数据用点子在平面坐标上表示出来。具体操作如下：

（1）收集数据。一般应收集30对以上两个变量对应的数据，数据太少，会导致判断不准确；数据太多，计算的工作量太大。

（2）画出横坐标x和纵坐标y，且它们的取值范围应包括数据的最大值与最小值。

（3）根据数据描出坐标点。如果有两组数据完全相同，则在点子上加一个圆圈（○）表示；如果有三组数据完全相同，则在点子上加两重圆圈（◎）表示，或用其他符号表示。把收集到的数据在坐标图上描点后即得到散布图，如图8.9所示。

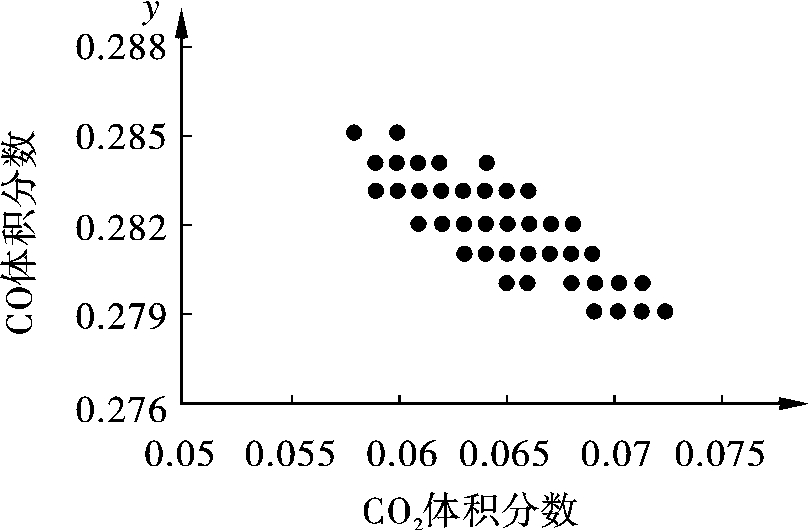
图8.9　散布图

8.3.6.3　散布图的观察与分析

即对照散布图的几种典型图例，判断两个变量之间是否相关以及属于哪一种相关关系。常见的散布图的几种典型形式如图8.10所示。

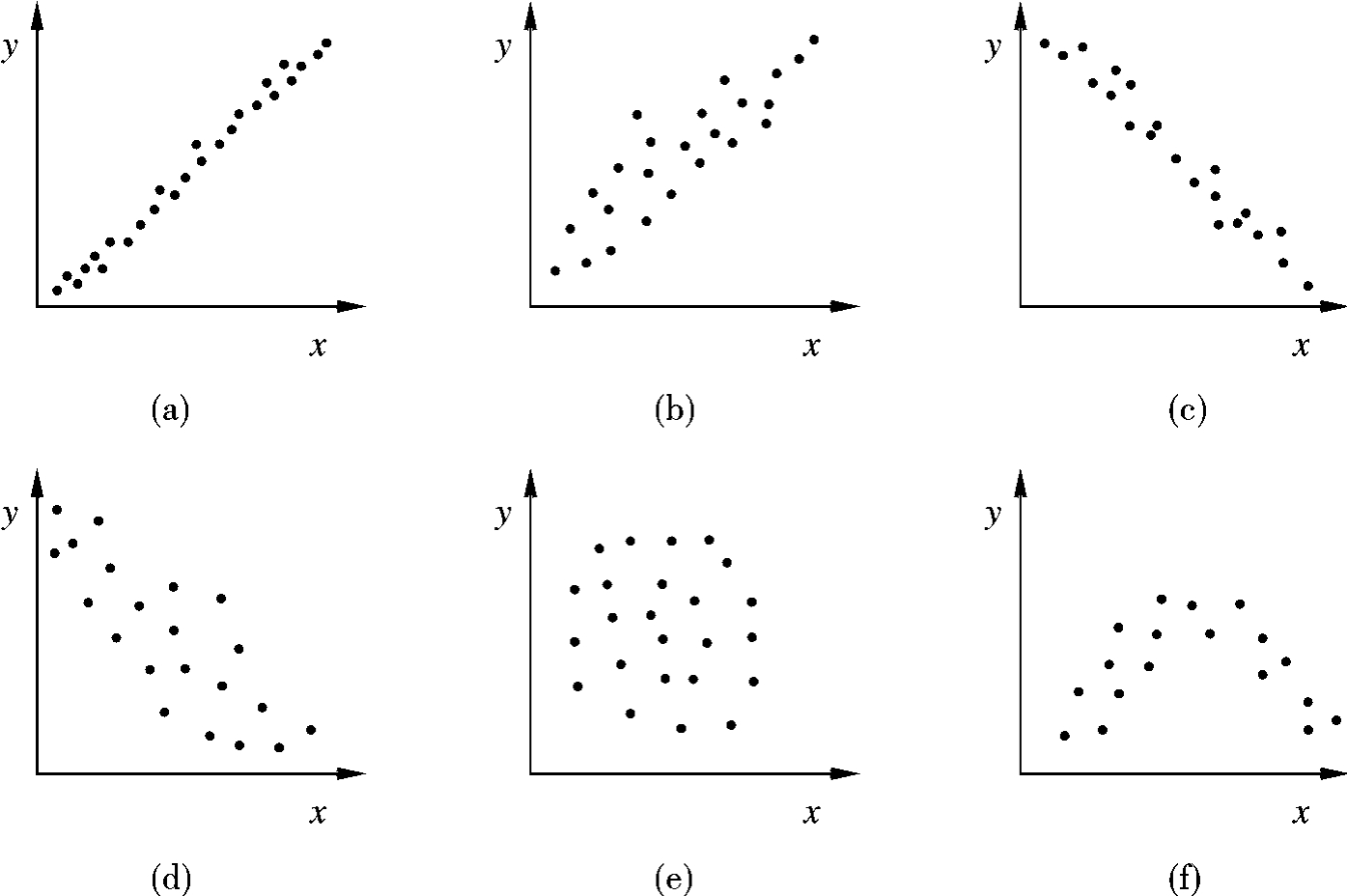
图8.10　散布图的典型形状

（1）强正相关　y随着x的增大而增大，且点分散程度小，如图8.10（a）所示。

（2）弱正相关　y随着x的增大而增大，且点分散程度大，如图8.10（b）所示。

（3）强负相关　y随着x的增大而减小，且点分散程度小，如图8.10（c）所示。

（4）弱负相关　y随着x的增大而减小，且点分散程度大，如图8.10（d）所示。

（5）不相关　y与x之间无明显规律，如图8.10（e）所示。

（6）非线性相关 y与x之间呈曲线变化关系，如图8.10（f）所示。

8.3.6.4　散布图的应用

散布图的应用分两步：一是作图观察，初步判断是否具有相关关系；若有相关关系则进一步判断相关程度如何，如果两个因素的相关程度很高，可用一个变量预测另一个变量或进行变量控制。具体应用如下：

（1）作散布图　已知某发酵食品中CO₂体积分数与CO体积分数有一定关系，收集的检测数据见表8.13，根据检测的50对数据作散布图如图8.9所示。

表8.13　某发酵食品中CO₂体积分数与CO体积分数数据表

(www.xing528.com)

续表8.13

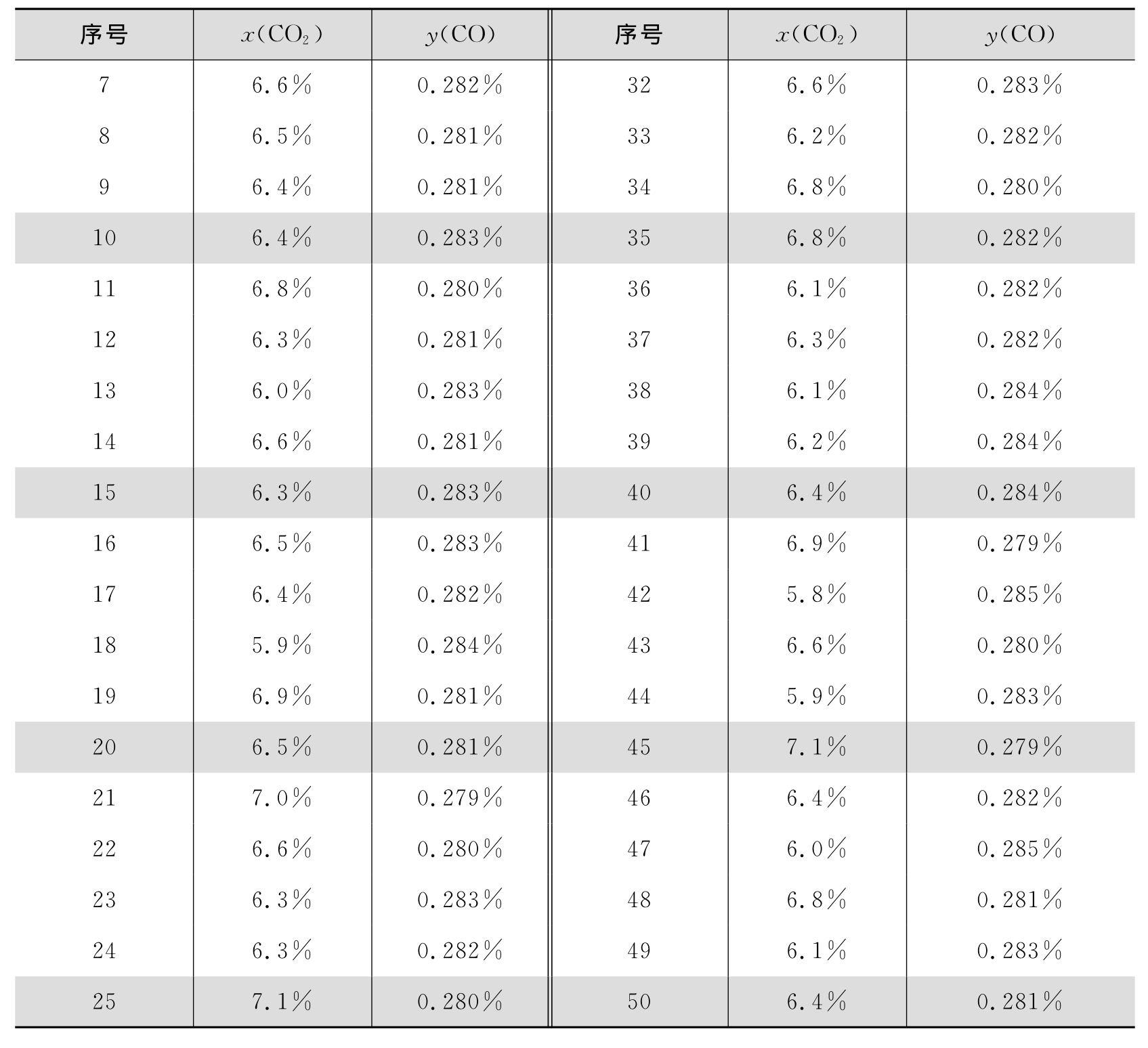
（2）散布图的观察与分析　由表8.13可以看出，CO体积分数随着CO₂体积分数的增加而减少，初步判断CO₂体积分数x与CO体积分数y之间存在负相关关系，若要进一步判断相关程度如何，可通过相关系数r的计算做定量分析。

（3）计算相关系数，确定相关程度　相关系数r的计算公式为：

本例计算结果为r＝－0.82，自由度为48时相关系数的临界值r_0.05（48）＝0.2732＜，可认为有95%的把握判定CO₂体积分数x与CO的体积分数y之间存在显著的负相关关系。

（3）预报与控制　利用散布图提供的信息求得变量x、y之间的回归直线方程用于质量控制，可通过回答以下两方面的问题实现质量控制：①对任何一个给定的观测点x₀，推断y₀大致落的范围；②若要求观测值y在一定的范围（如y₁＜y₀＜y₂）内取值，应将变量x控制在什么地方。前者就是所谓的预报问题，后者称为控制问题。

回归直线方程参数a、b的计算如下：

本例计算结果为a＝30.58，b＝0.37，则回归直线方程为：

y＝30.58－0.37x　　　　　　　　　　（8.15）

1）预报问题　当证明变量x和y的关系在统计上显著相关时才能进行问题的预报。一般来说，对于给定x₀处的观测值y₀：愈靠近回归直线的地方出现的机会愈大，离回归直线愈远的地方出现的机会越少，而且y₀的取值范围与回归直线标准差S_e之间存在下述关系：

y₀落在₀±3S_e范围内的可能性为99.7%；

y₀落在₀±2S_e范围内的可能性为95%；　

y₀落在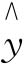₀±S_e范围内的可能性为68%。　

回归直线标准差的计算公式为：

利用y₀的取值范围与回归直线标准差S_e之间的关系，对于给定的x₀，就可预测在x＝x₀处的实际观测值y₀的分布范围及其可能性有多大，可通过在散点图上作两条与回归直线平行且等距的直线及回归直线控制图表示（图8.11）。本例中，当测得CO₂体积分数为6.6%时，若取3S_e，则CO的分布范围为：a＋bx－3Se＜y₀＜a＋bx＋3Se，即27.87%＜y₀＜28.41%，且其可能性为99.7%。

图8.11　回归直线控制图

2）控制问题　控制问题可以看做是预报的反问题。若要求观测值y₀在y₁～y₂范围内取值，则可从y₁＝a－3S_e＋bx₁（或y₁＝a－2S_e＋bx₁）及y₂＝a＋3S_e＋bx₂（或y₂＝a＋2S_e＋bx₂）中分别解出x₁、x₂，只要将x的取值控制在x1与x₂之间，就有99.7%（95%）的把握保证y₀在y₁～y₂范围内取值。

8.3.6.5　注意事项

①应将不同性质的数据分层后作散布图，否则将会导致判断错误。②散布图相关性规律的适用范围一般局限于观测值数据范围之内，不能任意扩大相关性判断范围。③散布图中出现的个别偏离分布趋势的异常点，应在查明原因后剔除。