网络环境下数字图书馆评价的理论和方法

第四节　网络环境下不同偏好信息的科技期刊选订方法

期刊是高校图书馆文献信息资源的重要组成部分。由于多种因素的影响，如重点学科建设、资金的供应、专业设置、教学、科研以及期刊利用率等等，各类高校图书馆都面临着一个值得深入研究的课题，即如何科学地选订馆藏科技期刊的问题。目前已有相关文献对此作了研究。王居平等^［78］把科技期刊选订视为一个多目标决策问题，提出一种新的科技期刊选订的最优组合赋权法决策方法。邵晋蓉等^［79］在对各种影响因素进行综合分析的基础上，采用优先关系法确定各种期刊关于某影响因素的二元优先关系对比矩阵，建立科技期刊优化配置模糊数学模型，从而达到选订的期刊排序方案。但是已有文献^{［78］［79］}均存在一些研究上的缺陷。《科技期刊选订的最优组合预测方法》一文中对选订的期刊由专家给出同一种决策信息，在此基础上，将不同的主、客观赋权法进行综合集成获得决策结果，因此该文对处理不同信息的决策问题是失效的；邵晋蓉等^［79］给出的二元优先关系对比判断矩阵的元素只能取0，0.5，1这三个值，显然这种信息标度并不能真正刻画两种方案的优先关系，因此邵晋蓉等^［79］给出的模型方法是不太细致的。

实际上如何科学地选订馆藏科技期刊是一个复杂的决策问题，因此需要多个专家进行群体决策。特别随着基于网络环境下的群决策支持系统的发展，迫切需要解决具有多种偏好信息的群决策理论。^［89］这是因为在实际的选订馆藏科技期刊的决策过程中，由于影响期刊多种因素的模糊性、不确定性以及专家知识结构和个人偏好等主客观因素的影响，专家对科技期刊的选订决策问题可能给出不同种类的偏好信息，如序关系值（或称“偏好次序值”）、效用值、互反判断矩阵、模糊互补判断矩阵等。^{［81－83］}因此我们有必要研究网络环境下不同偏好信息的科技期刊选订方法，这对高校图书馆文献信息资源的建设，提高期刊资源合理配置的效率具有重要的现实意义。反之，若我们不能对专家给出的不同种类的科技期刊的选订的信息进行有效的集成，则有可能造成误订或漏订，既影响文献利用效果，又造成人力、物力和财力资源的浪费。

本节在现有文献的基础上，首先给出专家在科技期刊的选订决策的问题过程中的其他3种偏好信息一致化为效用值的一种方法，然后从相对熵^{［84－85］}的概念出发，建立能够集结不同的偏好信息的群决策的最优化模型，最后以实例表明该方法的有效性和实用性。

一、馆藏科技期刊的四种偏好信息的描述

本节根据王居平、陈华友给出的科技期刊选订了4个决策指标：实用性、计划性、完整性和节约性。实用性含义指选择那些针对性强、受读者欢迎、实用性高的期刊；计划性的含义是指选订期刊要考虑到教学、科研发展的需要，要有预见性；完整性的含义是指选订期刊要完整且连续；节约性的含义是指两种期刊质量在相同的情况下应选择价格较低的那一种。

若某高校图书馆有4种可供选订的期刊，设A＝｛a₁，a₂，a₃，a₄｝为备选的期刊方案集，其中a_i表示第i种备选期刊，i＝1，2，3，4，设D＝｛d₁，d₂，d₃，d₄｝为专家集，其中d_k表示第k个专家，k＝1，2，3，4。这4位专家分别给出如下四种不同的偏好信息。具体简单描述如下：

（1）序关系值的偏好信息：

专家d₁根据个人的偏好直接给出备选期刊方案集A的次序：

O^（1）＝｛O^（1）（1），O（1）（2），O（1）（3），O（1）（4）｝＝｛3，1，4，2｝

其中O（1）（i）表示第i个备选期刊a_i的位置次序，i＝1，2，3，4。O（1）（i）越小，则备选期刊a_i综合评价越高。即在这4种可供选订的期刊中备选期刊a_i综合评价最高，它是排在第一位的，期刊a₄排在第二位，期刊a₁排在第三位，期刊a₃排在第四位。

（2）效用值的偏好信息：

专家d₂根据个人的偏好给出备选期刊方案集A的效用值：

U（2）＝｛u（2）（1），u（2）（2），u（2）（3），u（2）（4）｝＝｛0.5，0.7，0.9，0.1｝

其中u（2）（i）表示第i个备选期刊a_i的效用值，一般u（2）（i）越大，则备选期刊a_i越优。即在这4种可供选订的期刊中备选期刊a₃效用值最大，它是排在第一位的，期刊a₂排在第二位，期刊a₁排在第三位，期刊a₄效用值最小，排在第四位。

（3）互反判断矩阵的偏好信息：

专家d₃对A中方案进行两两综合比较，给出互反判断矩阵：

其中b^（3）_ij表示专家d3认为备选期刊a_i对比a_j的重要程度，且

b^（3）_ij∈［1/9，9］，b^（3）_ij·b^（3）_ji＝1，i，j＝1，2，3，4

专家d₃给出对方案集A中方案进行两两比较的互反判断矩阵

B（3），可按特征根法［28］计算B（3）的权向量：

W（3）＝（W（3）（1），W（3）（2），W（3）（3），W（3）（4））^T

它实际上是B（3）的最大特征根λ_max所对应的归一化特征向量。若在精度要求不高的条件下，也可以按方根法计算互反判断矩阵的归一化权向量，其计算公式［29］为：

由上式将第3位专家d₃给出的互反判断矩阵转化为备选的期刊方案集A的权向量，计算得：

W（3）＝（W（3）（1），W（3）（2），W（3）（3），W（3）（4））^T，

＝（0.2527　0.5009　0.1600　0.0863）^T

权向量体现了专家d₃按个人偏好对备选的期刊方案集A中4种备选的期刊重要性程度的认识。从计算结果可以看出，在这4种可供选订的期刊中备选期刊a₂的权系数最大，它是排在第一位的，期刊a₁排在第二位，期刊a₃排在第三位，期刊a₄排在第四位。

（4）模糊互补判断矩阵的偏好信息：

专家d₄对备选的期刊方案集A中方案进行两两比较的模糊偏好关系，它可由一个模糊互补判断矩阵P（4）＝（P_ij（4））_n×n＞A×A表达，相应的隶属函数为μ_P（4）∶A×A→［0，1］。

其中μ_P（4）（a_i，a_j）＝p_i^（_j4），p_i^（_j4）表示方案a_i优于方案a_j的程度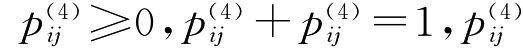，）＝0.5，i，j＝1，2，3，4

模糊互补判断矩阵的排序方法有很多。这里采用徐泽水［33］提出的模糊互补判断矩阵P（4）对应的排序权向量的一个简捷计算公式，即：

由上式计算得：

W（4）＝（W（4）（1），W（4）（2），W（4）（3），W（4）（4））^T

（0.2417　0.3000　0.2500　0.2083）

从计算结果可以看出，专家d₄认为在这4种可供选订的期刊中，备选期刊a₂排在第一位，期刊a₃排在第二位，期刊a₁排在第三位，期刊a₄排在第四位。

二、选订馆藏科技期刊的四种不同偏好信息的一致化

既然四位专家在科技期刊选订中给出不同形式的偏好信息，一般需要将不同种类的偏好信息都转化为同一种偏好信息，即必须进行信息的一致化后才能进行有效的信息集成。下面给出序关系值、互反判断矩阵、模糊互补判断矩阵均转化为效用值的方法。以下不妨假设专家d_k给出的某个备选期刊效用值满足非负性和归一化条件，即u^k（i）≥0，且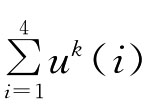＝1，k＝1，2，3，4

否则，对效用值进行归一化处理即可。

专家d₁给出序关系值的偏好信息转化为效用值的方法：

设O（1）（i）为专家d₁给出的第i个备选期刊a_i的位置次序，设u（1）（i）为a_i一致化后的效用值，如前所述，o^（1）（i）越小，备选期刊a_i越优，因此其对应的效用值u（1）（i）应越大，即u（1）（i）为o^（1）（i）的单调下降函数，可以取o^（1）（i）为如下形式：(www.xing528.com)

经过上式的转化，序关系值的偏好信息一致化为效用值，将第一位专家d₁给出的序关系值转化为效用值，计算得：

U（1）＝（u（1）（1），u（1）（2），u（1）（3），u（1）（4））^T＝（0.2 0.4 0.1 0.3）

显然一致化后的效用值满足非负性和归一化条件。

（2）专家d₂给出效用值的偏好信息归一化的方法：

由于专家d₂本来给的是效用值的偏好信息，因此只需将其归一化即可。为了统一记号，归一化后的效用值仍记为U（2），则有：

U（2）＝（u（2）（1），u（2）（2），u（2）（3），u（2）（4））

＝（0.2273　0.3182　0.4091　0.0455）

（3）专家d₃给出互反判断矩阵的偏好信息转化为效用值的方法：

专家d₃对备选的期刊方案集A的权向量体现了期刊重要性程度，并且权向量已满足非负性和归一化条件，因此只要令u（3）（i）＝W（3）（i），i＝1，2，3，4即可。所以有备选的期刊相应的效用值：

U（3）＝（u（3）（1），u（3）（2），u（3）（3），u（3）（4））^T

＝（0.2527　0.5009　0.1600　0.0863）^T

（4）专家d₄给出模糊互补判断矩阵的偏好信息转化为效用值的方法：

专家d₄对备选的期刊方案集A的权向量已满足非负性和归一化条件，因此只要令u^（4）（i）＝W（4）（i），i＝1，2，3，4，所以备选的期刊相应的效用值为：

U（4）＝（u（4）（1），u（4）（2），u（4）（3），u（4）（4））^T

＝（0.2417　0.3000　0.2500　0.2083）

三、不同偏好信息下期刊选订的相对熵信息集成的最优化方法

选订馆藏科技期刊是一个复杂的群体决策问题。群决策问题本质上是一个集结问题。^［84］为了获得一致的群体决策结果，就是要最小化群决策结果与个人偏好信息的不一致的可能性。而熵优化理论正好提供了一种较好的分析手段，为此引进离散形式的相对熵的性质：^［84］

若h（X，Y）＝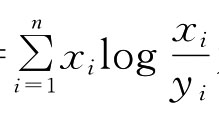

为X相对于Y的相对熵，则有：

（1）h（X，Y）≥0；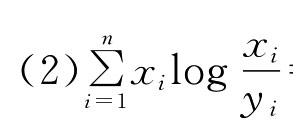

＝0当且仅当x_i＝y_i，i＝1，2，…，n。

其中X＝（x₁，x₂，…，x_n），Y＝（y₁，y₂，…，y_n）为两个离散概率分布。

该性质表明当X＝（x₁，x₂，…，x_n）和Y＝（y₁，y₂，…，y_n）完全相等时，X相对于Y的相对熵达到了最小值，因此可以用相对熵来度量两者的符合程度。

既然4种偏好信息一致化为效用值后，它们对应的效用值均满足非负性和归一化的条件，因此就可以将这些效用值作为专家对备选的期刊方案集A＝｛a₁，a₂，a₃，a₄｝的偏好信息评判的概率分布，假设各专家给出的概率分布是相互独立。

设4种备选期刊的信息集成后的效用值向量为Ug＝（u（1），u（2），u（3），u（4）），将它视为群体偏好信息评判值的一个概率分布。其中u（i）表示第i个备选期刊a_i的信息集成后的效用值，i＝1，2，3，4。设W＝（W₁，W₂，W3，W4）是专家集D＝（d₁，d₂，d₃，d₄）的权重向量，W_k表示专家d_k的权重，W_k越大，体现第k个专家越权威，k＝1，2，3，4。

根据相对熵的性质知，要想获得一致的4种备选期刊的信息集成后的效用值，就要最小化它与每一个专家给出的所有方案效用值向量的概率分布的相对熵，因此备选期刊选订中基于不同偏好信息的相对熵集成方法可以表示成如下最优化模型：

minF（u（1），u（2），u（3），u（4））＝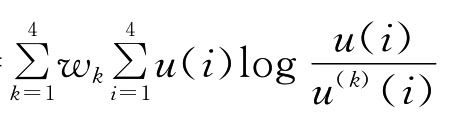

其中u（k）（i）表示专家d_k对第i个备选期刊a_i给出的偏好信息一致化后的效用值，Wk表示专家dk的权重。这里不妨假定专家的权重都相等，即：

W₁＝W₂＝w₃＝w₄＝1/4

u（i）表示第i个备选期刊a_i信息集成后的群效用值。上述最优化模型的解为：

由上式计算出4种备选期刊的一致化后效用值为：

u（1）＝0.2474，　　u（2）＝0.4009

u（3）＝0.2168，　　u（4）＝0.1349

根据计算出的最优4种备选期刊的一致化后效用值u（1），u（2），u（3），u（4）的大小对备选期刊方案集A进行排序得如下结果：

a₂＞a₁＞a₃＞a₄

其中“＞”表示“优于”的意思。

也就是说，综合4个专家的不同偏好信息，我们得出在这4种可供选订的期刊中，备选期刊a₂效用值最大，它是排在第一位的；期刊a₁排在第二位，期刊a₃排在第三位，期刊a₄效用值最小，排在第四位。因此我们可以根据经费的多少按着上述次序选订备选期刊。

本节给出了在网络环境下的处理不同形式偏好信息的科技期刊的选订方法。其特点包括两个方面：一是给出了选订馆藏科技期刊的4种不同偏好信息的一致化为效用值的简单方法；二是从相对熵的概念出发，建立集结不同的偏好信息一致化为效用值的馆藏科技期刊的最优化决策模型，并给出了最优化模型解的解析式，从而方便计算。实例分析结果表明本节提出的信息集成方法是有效的。