数字图书馆评价的理论方法：不确定性信息的应用

第五节　不确定性信息的数字图书馆馆藏评价方法及应用

多指标评价是对具有多个指标的有限方案，按照某种评价准则进行多方案选择和评价。通常，指标可分为效益型、成本型。所谓效益型指标是指指标值愈大愈优的指标，成本型指标是指指标值愈小愈优的指标。由于不同的指标往往具有不同的量纲和量纲单位，为了消除它们带来的不可公度性，在评价之前首先应将指标作无量纲化处理。在多指标评价中，通常把成本性指标转换为效益性指标再进行加权综合得出方案的评价结果。然而这不是唯一可行的方法。

由于数字图书馆是一个复杂的系统，且其评价问题面临不确定性环境，在实际的评价过程中，评价指标信息有时候以区间数形式来表达。因此有必要研究区间型不确定性多指标评价方法。本节在有序加权算术平均（OWA）算子和不确定组合加权算术平均（UCWA）算子的概念的基础上，探讨不确定性信息的数字图书馆馆藏评价方法，最后的实例结果表明该方法是可行的。

一、几个概念

定义5.5.1^［31］　记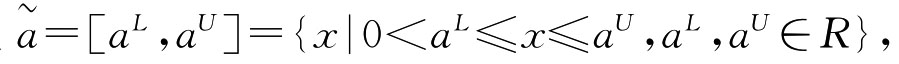

称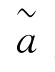为区间数，这里a^L，a^U分别为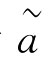的上界与下界。特别地当a^－＝a^＋时，则a退化为一个实数。

我们给出区间数的运算法则，^［31］其中区间数的加法、减法和乘法运算以及区间数大小比较的可能度的定义参见第三章第八节。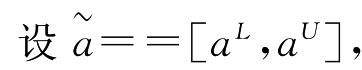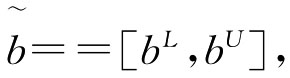且λ≥0，则有：

（1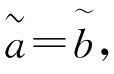当且仅当a^L＝b^L，a^U＝b^U。

（2＝［λa^L，λa^U，］，特别的，若λ＝0，则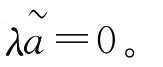

（3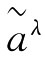＝［（a^L）^λ，（a^U）^λ］。定义5.5.2^［31］　设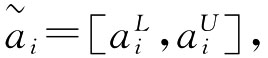i∈N＝｛1，2，…，n｝为n个区间数，令

则n阶矩阵P＝（p_ij）_m×n称为这n个区间数所确定的可能度矩阵，其中表示区间数的可能度。定义5.5.2表明可能度矩阵P的第i行第j列元素就是区间数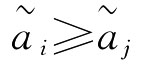的可能度，ｉ，ｊ＝１，２，…，ｎ。

实际上可能度矩阵的元素满足p_ij∈［0，1］，p_ij＋p_ji＝1，p_ii＝0.5，i，j＝1，2，…，n，因此矩阵P是一个模糊互补判断矩阵。模糊互补判断矩阵的评价方法有很多，这里采用徐泽水［31］提出的模糊互补判断矩阵P对应的评价向量的一个简捷计算公式：

由此得到P的一个评价向量V＝（v₁，v₂，…，v_n），称v_i为区间数所对应的权系数向量。即利用v_i可以对区间数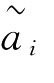进行大小评价，i＝1，2，…，n。

设Ω表示全体区间数的集合，则有如下定义：

定义5.5.3^［31］　设UWA：Ωⁿ→Ω，若

其中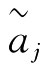∈Ω，W＝（W₁，W₂，…，W_n）是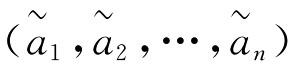的加权向量，

W_j∈［0，1］，j∈1，2，…，｛｝n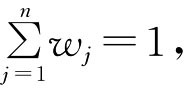

则称UWA是不确定加权算术平均算子。

定义5.5.4^［31］　设UOWA：Ωⁿ→Ω，若其中W＝（W₁，W₂，…，W_n）是与UOWA相关联的加权向量，W_j∈［0，1］，j∈1，2，…，

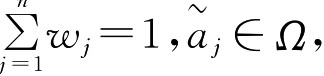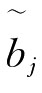｛｝n且是对区间数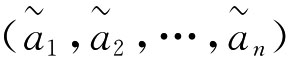进行大小评价的第j大元素，则称函数UOWA是不确定有序加权算术平均算子。

定义5.5.5^［31］　设UCWA：Ωⁿ→Ω，若

其中W＝（W₁，W₂，…，W_n）是与UCWA相关联的加权向量，W_j∈［0，1］，j∈1，2，…，

｛｝n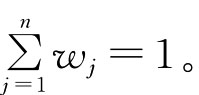且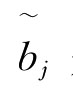是对一组加权区间数据组进行大小评价的第j大的元素，这里ω＝（ω₁，ω₂，…，ω_n）是数据组的加权向量，Wj∈［0，1］，j∈

1，2，…，｛｝n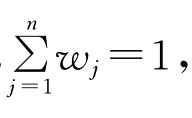，n是平衡因子。则称函数UCWA是不确定组合加权算术平均算子。

上述定义中权向量W＝（W₁，W₂，…，W_m）^T是可由模糊语义量化算子Q来确定的［53］，即：

其中

式中参数a，b，x∈［0，1］，对应于模糊语义量化准则的“大多数”、“至少半数”、“尽可能多”的Q的参数对（a，b）分别为（0.3，0.8），（0，0.5），（0.5，1）。

二、区间效益型指标和区间成本型指标的转化

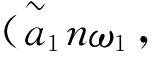
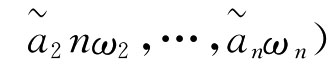
对于数字图书馆馆藏评价多指标评价问题，设X＝｛x₁，x₂，…，x_n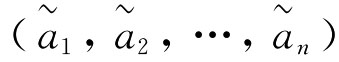｝为数字图书馆的方案集，U＝｛u₁，u₂，…，u_m｝为指标集。我们对方案x_i按指标u_j进行测度，得到x_i关于u_j的区间指标值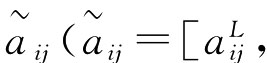a^U_ij］），从而构成区间评价矩阵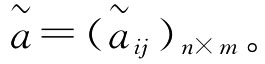为消除不同的物理量纲对评价结果的影响，须对不同的指标评价类型进行规范化处理。设I₁为效益型指标的下标集，I₂为成本型指标的下标集。

（1）对区间成本型指标转化为区间效益型指标，并进行如下规范化处理，即令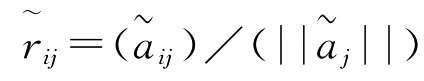：，其中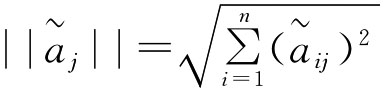，i∈｛1，2，…，n｝，

j∈I₁，按区间数的运算法则，则有：

（2）对区间效益型指标进行如下规范化处理，即令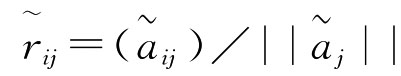：，其中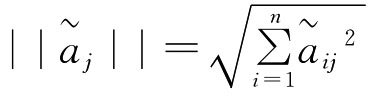，i∈｛1，2，…，n｝，

j∈I₂，按区间数的运算法则，则有：

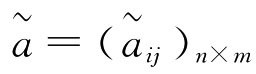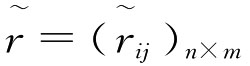这样我们将评价矩阵规范化为，其中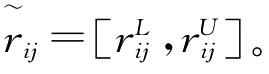

三、数字图书馆馆藏多指标群评价方法步骤

设D＝（d₁，d₂，…，d_t）为t位评价者集，X＝D＝｛x₁，x₂，…，x_t｝和U＝｛u₁，u₂，…，u_m｝分别为数字图书馆方案集和指标集。数字图书馆馆藏多指标群评价方法步骤如下：(www.xing528.com)

第一步：设评价者d_k∈D给出方案x_i∈X在指标u_j∈U下的指标值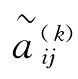，从而构成评价矩阵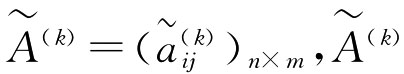中元素的物理量纲不同，则按上述式规范化处理得到规范化矩阵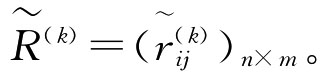

第二步：利用UOWA算子对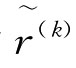中第i行进行集结，得评价者d_k对方案x_i的综合指标值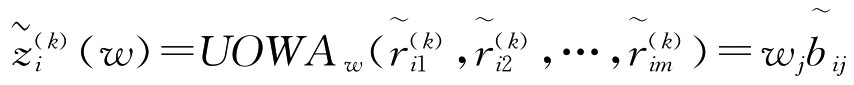：，i＝1，2，…，n，k＝1，2，…，t

其中W＝（W₁，W₂，…，W_n）是加权向量。

第三步：利用UCWA算子对计算的t位评价者给出的方案x_i的综合指标值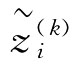（W）进行集结，得到方案x_i的群体综合评价指标值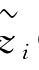（λ，W′）：

（W），i＝1，2，…，n

其中W′＝（W′₁，W′₂，…，W′_t）是UCWA算子的加权向量，W′_k∈［0，1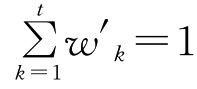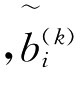］，是一组加权数据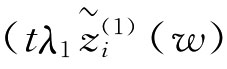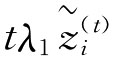，…（W））中第k大的元素；λ_k∈［0，1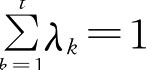］，t是平衡因子，λ＝（λ₁，λ₂，…，λ_t）是t位评价者的权重向量。

第四步：对各方案的综合指标值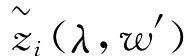进行方案评价。因为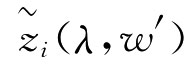体现为区间效益型指标，所以计算其值越大表示方案越优。

四、数字图书馆馆藏多指标评价的实例分析

设有四个备选数字图书馆方案x_i（i＝1，2，3，4）可以选择，数字图书馆馆藏评价由7个指标进行评价，这7项指标分别是：

（1）可靠性，要求数字图书馆的馆藏资源本身客观、真实。

（2）合理性，要求数字图书馆的馆藏资源公正、适度、一致。

（3）可用性，要求数字图书馆的馆藏资源符合用户的实际需要，并可异地访问与统计。

（4）全面性，要求数字图书馆的馆藏资源收录范围全面、广泛。

（5）权威性，要求数字图书馆网站和馆藏具有声望或权威，并拥有知识产权。

（6）时效性，要求馆藏信息能始终保持最新状态，定期更新。

（7）经济性，要求用最少的费用支出满足用户对馆藏信息的需求。

现有三位评价者d_k（k＝1，2，3），权重向量为λ＝（0.4，0.3，0.3）。依据上述指标对每个数字图书馆分别打分，得到3个不确定性信息评价矩阵，如表5.5.1、表5.5.2和表5.5.3所示。现在来确定最佳的数字图书馆方案。

表5.5.1　评价者d₁给出的不确定性信息评价矩阵

表5.5.2　评价者d₂给出的不确定性信息评价矩阵

表5.5.3　评价者d₃给出的不确定性信息评价矩阵

第一步：评价者给出的指标为效益型，进行规范化处理得：

第二步：利用UOWA算子，对矩阵的每一行进行集结，这里UOWA算子的权重向量可以按模糊语义量化准则“至少半数”取（a，b）＝（0，0.5），从而求得权向量：

W＝（0.2857，0.2875，0.2875，0.1429，0，0，0）

则有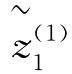：（W）＝［0.5074，0.5555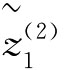］（W）＝［0.5253，0.5907］

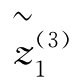（W）＝［0.5105，0.5842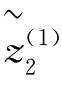］（W）＝［0.5017，0.5495］

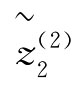（W）＝［0.5341，0.5869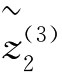］，（W）＝［0.5007，0.5651］

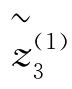（W）＝［0.5351，0.5857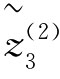］，（W）＝［0.4715，0.5295］

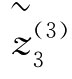（W）＝［0.4515，0.5021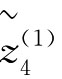］，（W）＝［0.5203，0.5649］

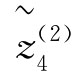（W）＝［0.5105，0.5814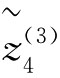］，（W）＝［0.5206，0.6131］

第三步：利用UCWA算子对3位评价者给出的每个方案的综合指标值进行集结。由此计算得到每个方案的群体综合指标值，λ＝（0.4，0.3，0.3），UCWA算子的权重向量可以按模糊语义量化准则，“至少半数”取（a，b）＝（0，0.5），从而求得W＝（0.67，0.33，0），则有：（λ，W′）＝［0.5781，0.6539］（λ，W′）＝［0.5806，0.6439］（λ，W′）＝［0.5164，0.5779］（λ，W′）＝［0.5747，0.692］

第四步：求出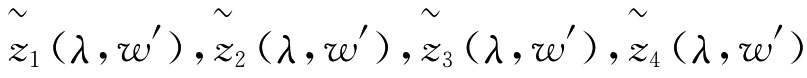四个区间数所确定的可能度矩阵为：

然后我们求得模糊互补判断矩阵P的评价向量为

v＝（0.2975，0.2689，0.1250，0.3086）

注意到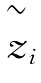（λ，W′）为区间效益型指标，所以其对应的权系数越大表示方案越优。所以x₄＞x₁＞x₂＞x₃。