第八节 指标值为区间型的多指标数字图书馆评价方法
由于数字图书馆的复杂性和不确定性，以及人类思维的模糊性，评价者往往不能明确地给出指标的具体数值，而是以区间数的形式来表达。本节针对指标权重已知而指标值为区间数的多指标数字图书馆评价问题提出了一种基于区间数的可能度的评价方法。这种方法的优点是思路清晰，方法简洁、合理，并易于在计算机上操作，为解决数字图书馆评价中指标值以区间数形式给出的多指标评价问题提供了一条新思路。
一、评价方法的基本原理
设多指标数字图书馆评价问题有m个目标G1，G2.…，Gm和n个评价方案A1，A2，…，An，设方案Ai（i＝1，2，…，n）在目标Gj（j＝1，2，…，m）下的指标值为区间数aij，其中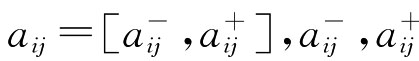
为确数，且
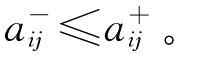称矩阵A＝（aijn×m）为评价矩阵。最常见的指标类型有效益型和成本型两种，设Ii（i＝1，2）分别表示效益型和成本型指标的下标集，且令M＝｛1，2，…，m｝，N＝｛1，2，…，n｝。为了消除不同物理量纲对评价结果的影响，必须对评价矩阵进行规范化处理。
1.有关区间数的运算及序关系［31］
设a＝［a－，a＋］，b＝［b－，b＋］为两区间数，则有：
（1）a±b＝［a－±b－，a＋±b＋］
（2）ab＝［a－b－，a＋b＋］，特别地λa＝［λa－，λa＋］，λ＞0
（3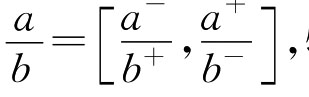
特别地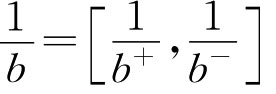
（4）a≤b→a－≤b－，a＋≤b＋
根据区间数运算法则，通过下面的变换：［31］
其中
可将评价矩阵A转化为矩阵C：
其中
从而易得0≤c－ij≤1，而c＋ij有可能大于1，可用下面的变换将矩阵C规范化，得到规范化矩阵R＝（rij）m×n，其中
易知
定义3.8.1 称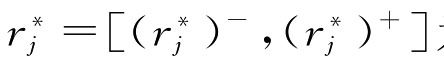
为目标Gj（j∈M）下的理想指标值，若
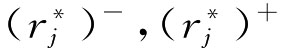满足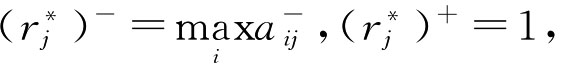
则由理想指标值构成的方案称为理想方案，用A＊表示。
由区间数的运算知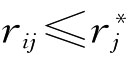
（i∈N，j∈M）
在指标权重W的作用下，构造矩阵（矩阵元素为区间数）
G1 G2 … Gm
并称之为“单边增广加权规范化评价矩阵”。
定义3.8.2［31］ 设a＝［a－，a＋］，b＝［b－，b＋］，且记L（a）＝a＋－a－，L（b）＝b＋－b－，则称
为a≥b的可能度。
根据多指标评价分析中的简单加权法，令
则ei表示方案Ai的综合指标值，e表示理想方案A＊的综合指标值，显然ei越大，方案Ai越优，且ei≤e（i∈N）。
2.评价方法的计算步骤
实际上，可以证明若a＝［a－，a＋］，b＝［b－，b＋］为两区间数，b不变，则p（a≥b）是a的单调非减函数。(www.xing528.com)
令gi＝p（ei≥e），i∈N，易知0≤gi≤1，gi越大，ei越大，方案A越优，因此可以按照gi的大小来确定方案Ai的排序。
综上所述，评价方法的计算步骤如下：
（1）根据评价目标的类型构造规范化评价矩阵R＝（rij）n×m；
（2）在给定指标权重W＝（W1，W2，…，Wm）下，构造单边增广加权规范化评价矩阵E；
（3）由单边增广加权规范化评价矩阵E，计算ei（i∈N）及e，进而求出可能度gi（i∈N）；
（4）根据可能度gi（i∈N）的大小对相应方案进行排序。
二、数字图书馆评价的算例分析
设有五个数字图书馆A1，A2，A3，A4，A5，各数字图书馆的指标值为区间数，列于“表2.8.1”：
表3.8.1 各数字图书馆的指标值
现用熵值法确定四个指标的权系数。在四个指标中，指标2、指标3为效益型目标；指标1、指标4为成本型目标，权重向量已知，权重向量W＝（0.150，0.200，0.200，0.450）。
利用上述方法求出四个指标的权重。具体步骤如下：（1）根据评价指标类型构造规范化评价矩阵R。
由“表3.8.1”中的数据建立原始评价矩阵如下：
将评价矩阵A转化为矩阵C：
将矩阵C规范化，得到规范化矩阵：
（2）给定加权向量W＝（0.150，0.200，0.200，0.450），构造单边增广加权规范化矩阵E。
由规范化矩阵R知：
A＊＝（［0.6944，1.0000］，［0.5625，1.0000］，［0.5102，1.0000］，［0.2500，1.0000］）
再由单边增广加权规范化矩阵的定义知：
（3）由单边增广加权规范化评价矩阵E知：
e1＝［0.3584，0.9214］， e2＝［0.3116，0.6550］， e3＝［0.3529，0.8929］
e4＝［0.3126，0.6383］， e5＝［0.2856，0.6993］， e3＝［0.4312，1.0000］再由可能度公式得：
g1＝0.4331，g2＝0.2453，g3＝0.4164，g4＝0.2315，g5＝0.2729
（4）由gi的大小得方案的排序为：
A1＞A3＞A5＞A2＞A4
从上例可以看出，本节提出的区间数评价矩阵排序的方法是有效且可行的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
