数字图书馆评价：模糊层次分析法成果

第二节　模糊层次分析法（FAHP）

模糊性是人类思维和客观事物普遍存在的属性之一。这不仅是因为在人类活动过程中存在着大量的难以精确定量描述的评价问题，而且，在人类思维活动中，人们又大多用模糊语言来交流思想，互通信息，然后进行推理分析，综合评判，最后做出评价。这种带有模糊性的直觉与逻辑推理能力，是人类思维活动的特征。因此，在评价研究中引入模糊技术是合理的，也是必要的。其次，由于评价问题的复杂性和评价者知识的缺乏，所以，已知的评价信息很有可能具有不精确性和模糊性。因此，研究基于模糊评价信息的评价技术是十分必要的。模糊集合理论对表达评价信息的不精确性提供了灵活性，借助于模糊理论可以研究许多评价问题，所以有必要将模糊技术与评价方法相结合。因此，在传统的AHP中引入模糊的思想，这样就出现了基于模糊互补判断矩阵的具有层次结构的评价问题。因此，有关模糊层次分析法^［31］（FAHP）的研究，近年来受到了国内外学者的重视，目前，在有关互补判断矩阵的排序方法的研究中，已经有十多种方法被提出。但是在已有的研究成果的基础上，如何解决具有层次结构的评价问题，这是一个值得重视的课题。

一、FAHP评价分析的步骤

FAHP与传统的AHP有许多相似之处。本质上也是一种评价思维方式，它的理论核心是将复杂的系统简化为有序的递阶层次结构；但是他们所不同的是FAHP是基于两两评价方案比较的模糊互补判断矩阵的形式，采取的具体分析方法与AHP有不同之处。

一般地，利用FAHP进行评价分析可分为如下三个步骤：

第一步：建立层次结构模型。

应用FAHP方法对社会、经济和管理领域的问题进行多目标评价，首先要把问题条理化和层次化，构造出能够反映系统本质属性的内在联系的递阶层次结构模型。在这种层次结构模型中，根据系统分析的结果，弄清系统与环境的关系、系统所包含的因素、因素之间的相互联系和隶属关系等，将具有共同属性的元素归并为一组，作为结构模型的一个层次；同一个层次的元素既对下一层次起着制约作用，同时又受到上一层次元素的制约。这样就构造了递阶层次结构模型。一般来说，可以将层次分为三种类型：

（1）最高层。只包含一个元素，表示评价分析的总目标。因此，也称为“总目标层”。

（2）中间层。包含若干层元素，表示实现总目标所涉及的各子目标，包括各种准则、约束、策略等。因此，也称为“目标层”。

（3）最低层。表示实现各评价目标的可行方案、措施等，也称为“方案层”。

第二步：按照层次结构模型，从上到下逐层构造判断矩阵。

每一层元素都以相邻上一层次各元素为准则，构造两两比较构造判断矩阵。设一个有限的评价方案集为X＝｛x₁，x₂，…，x_n｝，评价者针对某个准则H，对方案集X中的任意两个方案x_i和x_j的优劣关系进行判断，给出比较信息，可用确定的数值表示，也可用模糊信息形式表示。得到下面的判断矩阵：

这里，元素b_ij表示方案x_i优于方案x_j的程度，且

①b_ij＝0.5表示方案x_i和方案x_j同样重要；

②0≤b_ij＜0.5表示方案x_j比方案x_i重要，数值越小，方案x_j比方案x_i越重要；

③0.5＜b_ij≤1表示方案x_i比方案x_j重要，数值越大，方案x_i比方案x_j越重要。

为表述方便，须引进模糊互补判断矩阵的概念。

定义3.2.1^［31］　若矩阵B＝（b_ij）_n×n满足如下两个条件：

（1）b_ii＝0.5，A i∈｛1，2，…，n｝

（2）b_ij＋b_ji＝1，b_ij≥0，A i，j∈｛1，2，…，n｝则称B为模糊互补判断矩阵。

第三步：计算层次单排序权重。

二、FAHP的几种比较重要的排序方法

根据实际情况，通过求解所构造的模糊互补判断矩阵来得到排序权重，权重越大，相应元素越重要。下面分别简单介绍几种比较重要的排序方法。

（1）方法一：^［32］

对模糊互补判断矩阵B＝（b_ij）_m×n按行求和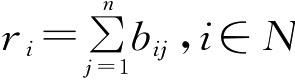，并进行数学变换：

其中a＝2（n－1），得到模糊一致性矩阵R＝（r_ij）_m×n。令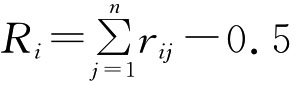，则对R_i归一化求得排序向量为W＝（W₁，W₂，…，W_n）^T，满足

或者

式中

（2）方法二：^［33］

对矩阵B＝（b_ij）_m×n中的元素按行求和，可得

并施以以下数学变换(www.xing528.com)

可得到具有完全一致性得判断矩阵R＝（r_ij）_n×n，对矩阵R采用行和归一化，可得到排序向量W＝（W₁，W₂，…，W_n）^T为：

（3）方法三：权的最小平方法。^［34］由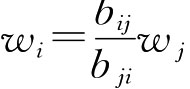代入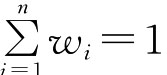，得到一致性互补判断矩阵排序的精确解

由于决策者在实际决策时所给出的互补判断矩阵往往是非一致的，为此构造如下带有偏差函数的最优化模型：

模型的最优解即为合理的排序向量，这种方法称为“权的最小平方法”。

（4）方法四：特征向量法（CEM）。^{［28］［29］}

也可以利用AW＝λ_maxW来求解向量W，式中λ_max是互反判断矩阵A的最大特征值，W为A的最大特征值所对应的特征向量，归一化后就是A的排序向量，显然，它也是B的排序向量，这种排序方法称为“特征向量法”（CEM）。

（5）方法五：最小偏差法（LVM）。^［35］

若模糊互补判断矩阵B满足完全一致性条件，矩阵B中的元素满足：

b_ij＝W_i－W_j＋0.5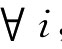，，j∈｛1，2，…，n｝

为了确定W_j，可构造如下最优化模型

解此最优化问题，可得出方案的排序向量W＝（W₁，W₂，…，W_n）^T为

（6）方法六：^［36］

当矩阵B不具有完全一致性时，为了使b_ij逼近于（1＋W_i－W_j）/2，即希望确定W_j，使之满足

由上式可构造如下多目标最优化模型｝

minz_ij＝｜b_ij－（0.5＋0.5W_i－0.5W_j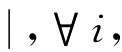），j∈｛1，2，…，n｝，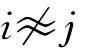

以上模型可转化为下面得线性目标规划问题：

式中,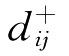是目标函数z_ij高于期望值0的上偏差变量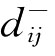，是目标函数z_ij低于期望值0的下偏差变量。

（7）方法七：^［37］

若模糊互补判断矩阵B满足完全一致性条件，则下式成立：

根据上式可得到：

（1－b_ij）W_i＝b_ijW_j，i，j∈｛1，2，…，n｝

为了确定W_j，可构造如下多目标最优化模型：上述最优化模型可转化为下面的线性目标规划问题：

式中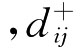是目标函数z_ij高于期望值0的上偏差变量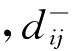是目标函数z_ij低于期望值0的下偏差变量。

（8）方法八。^［38］

构造如下最优化模型

解此最优化问题，可以得出方案的排序向量为：

三、层次总排序

层次总排序是从上到下逐层进行的。在实际计算的时候，为了方便，一般按表格形式计算。设相邻两层次中，层次A包含有m各元素A₁，A₂，…，A_m，层次B包含n个元素B₁，B₂，…，B_n。上一层次元素总排序权重分别为v₁，v₂，…，v_n，下一层次元素关于上一层次元素A_j的层次单排序权重向量为（b_1j，b_2j，…，b_nj）^T。层次B的总排序权重值计算由“表3.2.1”给出。

表3.2.1　FAHP总排序权重值计算