数字图书馆评价权重确定方法

第四节　数字图书馆评价中权重的确定方法

一、熵值法在确定数字图书馆评价指标权重中的应用

在信息论中，熵值是系统无序程度或混乱程度的度量，信息被解释为系统无序程度的减少，信息表现为系统的某项指标的变异度。即系统的熵值越大，则它所蕴涵的信息量越小，系统的某项指标的变异程度越小；反之，系统的熵值越小，则它所蕴涵的信息量越大，系统的某项指标的变异程度越大。

熵值法在确定数字图书馆评价指标权重中应用的一个基本思想是：信息表现为数字图书馆评价的某项指标的变异度。即数字图书馆评价的指标熵值越大，则它所蕴涵的信息量越小；数字图书馆评价的某项指标的变异程度越小，则该指标的在数字图书馆评价中对应的权系数就越小。反之，数字图书馆评价的指标的熵值越小，则它所蕴涵的信息量越大，即某项指标的变异程度越大，则该指标在数字图书馆评价中对应的权系数就越大。

设现有m个数字图书馆评价方案，n个数字图书馆评价指标，设矩阵C＝（x_ij）_m×n表示数字图书馆评价矩阵，其中x_ij表示第i个数字图书馆方案在第j个评价指标下的指标值。

用熵值法确定数字图书馆评价的指标权重的步骤如下：

（1）将各种数字图书馆评价方案中指标序列单位化。即：

显然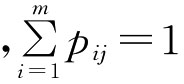，j＝1，2，…，n。

（2）计算第j个数字图书馆评价指标的熵值h_j：

其中k＞0为常数，ln为自然对数，h_j≥0，j＝1，2，…，n。

如果p_ij全部相等，即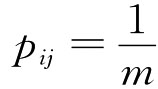，j＝1，2，…，n，那么h_j取极大值，即

0≤h_j≤1，j＝1，2，…，n

（3）计算第j种评价指标序列的变异程度系数d_j：

因为0≤h_j≤1，根据数字图书馆评价的某项指标的熵值的大小与其变异程度相反的原则，所以定义第i种指标序列的变异程度系数d_i为：

d_j＝1－h_j，j＝1，2，…，n

（4）计算指标各评价指标的权重W₁，W₂，…，W_n

上式体现了一个原则：某个指标序列的变异程度越大，则其在数字图书馆评价中对应的权重就越小。且权系数满足：

（5）计算数字图书馆评价方案的综合评价值x_i：

二、熵值法在确定数字图书馆评价中指标权重的应用实例分析

设有6种数字图书馆建设方案，数字图书馆评价指标有4种，包括内容评价指标、技术评价指标、服务评价指标、法律和效益评价指标方面。内容评价指标用于反映数字图书馆内容的权威性、准确性、新颖性、时效性、完备性、适用性等；技术评价指标用于反映数字图书馆智能检索技术、传输速度快捷性、网站稳定性、多语言技术等；服务评价指标用于反映数字图书馆的读者群对该数据库的满意程度、读者使用率、人均使用次数、人均全文下载量、资源可获得性等；法律和效益评价指标用于反映数字图书馆的知识产权保护、合理使用图书馆“特权”、数据库价格和价格上涨幅度、使用成本、收益核算等。

采用专家打分法，采用百分制得到6种数字图书馆建设方案的4种评价指标评价值。x_ij表示第i个数字图书馆方案在第j个评价指标下的指标值（i＝1，2，3，4，5，6，j＝1，2，3，4），用矩阵C表示，C值如下：

根据熵值法确定4种评价指标的权系数的原理，其计算步骤如下：

（1）各指标同度量化，计算第j种指标下第i种期刊指标值的比重p_ij：

即：

同理得：

p₂₁＝0.2141，p₃₁＝0.1940，p₄₁＝0.2116，p₅₁＝0.0882，p₆₁＝0.0756，p₁₂＝0.1951，p₂₂＝0.1931，p₃₂＝0.1280，

p₄₂＝0.1748，p₅₂＝0.1585，p₆₂＝0.1504，p₁₃＝0.1934，

p₂₃＝0.0552，p₃₃＝0.1105，p₄₃＝0.1823，p₅₃＝0.2210，

p₆₃＝0.2376，p₁₄＝0.2019，p₂₄＝0.1671，p₃₄＝0.1555，

p₄₄＝0.1137，p₅₄＝0.1856，p₆₄＝0.1763

（2）计算第j种指标的熵值h_j为：

其中ln为自然对数，即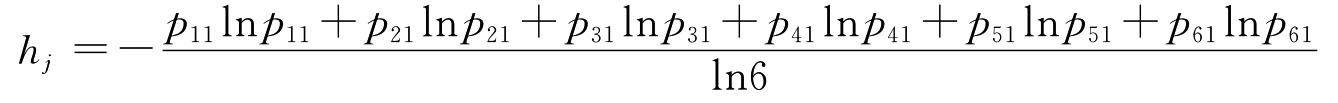：＝0.9585

同理得：

h₂＝0.9942，h₃＝0.9524，h₄＝0.9918

（3）计算第j种指标的差异性系数程度系数为d_j＝1－h_j，j＝1，2，3，4。

即：

d₁＝1－h₁＝1－0.9585＝0.0415

同理得：

d₂＝0.0058，d₃＝0.0476，d₄＝0.0082

（4）计算4种评价指标的权系数W j为: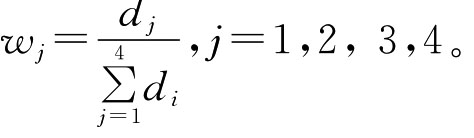

即：

同理得：

W₂＝0.0562，　W₃＝0.4615，　W₄＝0.0794

三、数字图书馆评价中的最优组合赋权方法

对于数字图书馆评价问题，无论采取什么样的求解方法，一般需要确定各指标的相对重要程度，而重要程度往往用指标的权系数来反映，权系数越大则其对应的指标就越重要。因此，权系数的正确确定，对于数字图书馆评价问题的正确评价具有十分重要的作用。

目前数字图书馆评价中指标权重确定有多种方法。大体上可分为主观赋权方法和客观赋权方法两大类。^［25］主观赋权法是评价者根据经验主观判断或各指标的主观重视程度进行赋权的方法，如专家调查法、二项系数法、AHP法等；而客观赋权法是通过建立一定的数学模型计算出权重系数，如主成分分析法、熵技术法、均方差法及目标规划法等。

两大类赋权方法各有不同的特点。主观赋权法的随意性较大，评价准确性和可靠性稍差一些，这是其不足之处。但指标的相对重要程度一般不会违反人们的常识。客观赋权法显著的特点是存在赋权的客观标准，通过计算得出评价指标的权重系数，而不是人为给定的。但客观赋权法的缺点是有时计算结果无法解释。

1.最优组合赋权方法的基本原理

设有某个数字图书馆评价问题，其数字图书馆评价方案集表示为S＝｛S₁，S₂，…，S_m｝，其指标集表示为P＝｛P₁，P₂，…，P_n｝，第i个方案S_i对第j个指标P_j的指标值记为a_ij，i＝1，2，…，m，j＝1，2，…，n，矩阵A＝（a_ij）_m×n称为“评价矩阵”。

通常，指标可分为效益型、成本型。所谓效益型指标是指标值愈大愈好的指标，成本型指标是指标值愈小愈好的指标。由于不同的指标往往具有不同的量纲和量纲单位，为了消除它们带来的不可公度性，在评价之前首先应将指标作无量纲化处理。然而，评价指标类型不同，无量纲化处理方法也将不同。

对于效益型指标，一般可令：

对于成本型指标，一般令：

式中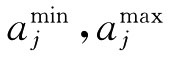分别为第j个指标P_j的最小值和最大值。

显然，b_ij∈［0，1］，i＝1，2，…，m，j＝1，2，…，n

上述的无量纲化处理的矩阵B＝（b_ij）_m×n称为“规范化的评价矩阵”，b_ij表示第i个评价方案S_i对第j个指标Pj的规范化指标值，矩阵B的第i行表示第i个评价方案S_i对n个指标值的规范值。显然b_ij愈大愈好。

不管是主观赋权方法还是客观赋权方法，前已指出它们均有若干具体的赋权方法。假设某个数字图书馆评价，对n个指标有l种具体的赋权方法对其赋值。设第k种赋权方法给出的权向量值为：

W_k＝（W_1k，W_2k，…，W_nk）^T，k＝1，2，…，l

其中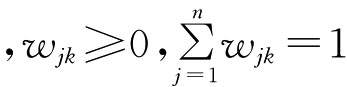，k＝1，2，…，l，j＝1，2，…，n。

为了综合各种赋权方法的特点，可考虑如下组合赋权W_c＝（W_c1，

W_c2，…，W_cn）^T，令

W_c＝λ₁W1＋λ₂W₂＋…＋λ_lW_l

称W_c＝（W_c1，W_c2，…，W_cn）^T为组合赋权系数向量。其中λ₁，λ₂，…，λ₁为组合权系数向量的线性表出系数。λ_k≥0，k＝1，2，…，l，且满足单位化约束条件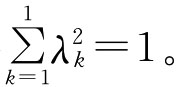

令分块矩阵W＝（W₁，W₂，…，W1），Λ＝（λ₁，λ₂，…，λ₁）^T，则称W为l个权系数向量组成的矩阵。W实际上为n×l的矩阵，Λ为组合权系数向量的线性表出系数组成的l维列向量。此时可表为矩阵形式(www.xing528.com)

W_c＝WΛ

Λ^T＝1Λ

根据简单线性加权法，由组合赋权系数向量W_c计算而得的第i个数字图书馆评价方案S_i的多指标综合评价值可表示为

一般而言，D_i（W_c）总是愈大愈好，D_i（W_c）愈大表示第i个数字图书馆评价方案S_i愈优。但是在多指标评价中，如果各指标的权系数确定不当，会致使各数字图书馆评价方案的多指标综合评价值D_i（W_c）（i＝1，2，…，m）互相差别很小，这样将不利于数字图书馆评价方案的排序。所以选择组合赋权系数向量的一个基本思想是使各数字图书馆评价方案的多指标综合评价值D_i（W_c）尽可能分散，越分散越有利于方案的评价与排序。采用中，把各数字图书馆评价方案多指标综合评价值的离差平方和作为其分散程度的度量。为此定义第i₁个数字图书馆评价方案综合评价值D_i1（W_c）和第i₂个数字图书馆评价方案综合评价值D_i2（W_c）的离差为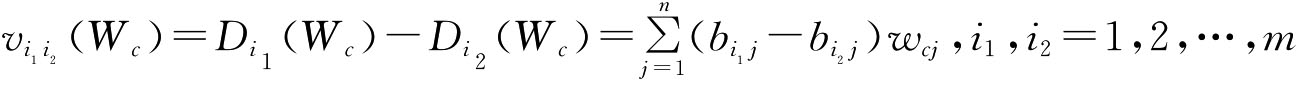

设v_i（W_c）表示第i个数字图书馆评价方案与其他各数字图书馆评价方案综合评价值的离差平方和，则有

根据前述的选择组合赋权系数向量Wc的基本思想，应该使m个数字图书馆评价方案总的离差平方和达到最大，这样有利于方案的评价与排序。于是可构造如下目标函数：

若令n×n阶矩阵B1为

则目标函数J₁（Wc）可表为

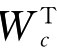J₁（Wc）＝B1Wc

其中Wc＝（W_c1，W_c2，…，W_cn）^T为组合赋权系数向量。

要想求出组合赋权系数向量W_c，只要求出组合权系数的线性表出系数向量Λ就行了。既然W_c为Λ的函数，从而表明目标函数J₁（W_c）也为Λ的函数，此时J₁（W_c）可记为F（Λ）。于是基于m个数字图书馆评价方案总的离差平方和的最优组合赋权方法可表示为如下最优化问题：

maxF（Λ）＝Λ^TW^TB₁WΛ

对于上述模型，先不考虑Λ的非负性，最优化问题可简化为无约束优化问题：

对于上式，我们有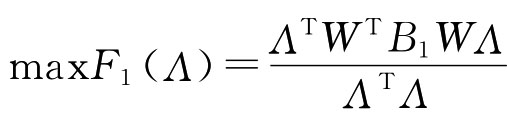＝λ_max，最优解λ^＊为λ_max对应的单位化特征向量。其中λ_max为矩阵W^TB₁W的最大特征根。

因此F₁（Λ）最大值为对称矩阵W^TB₁W的最大特征根，最优解Λ^＊为矩阵W^TB₁W的最大特征根所对应的单位化特征向量。

因为矩阵WTB₁W是对称非负定的，根据非负不可约矩阵的Per‐ron－Frobenius定理，λ_max为单根，且它对应的Λ^＊的分量全部为正，因此Λ^＊也是模型的最优解。求解WTB₁W的最大特征根所对应的单位化特征向量Λ^＊，可以采用现成的计算软件，如MATLAB^［26］。Λ^＊求出以后，即得最优组合赋权系数向量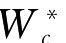＝WΛ^＊。

由于传统的加权向量一般都是满足归一化约束条件，因此为了与人们的习惯用法保持一致，还需要对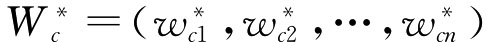进行归一化处理。即令

当然也可以先对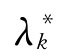，k＝1，2，…，l进行归一化处理，即令

再按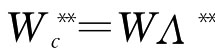计算加权向量。

综上所述，最优组合赋权系数向量的计算步骤可归纳为：

第一步：由指标矩阵A＝（a_ij）_m×n计算规范化的指标矩阵B＝（b_ij）_m×n，以及根据定义式计算n阶对称非负定方阵B1。

第二步：由l种具体不同的赋权方法组成的权系数向量矩阵W和B1计算对称矩阵WTB1W，同时计算WTB1W的最大特征根λmax及其所对应的单位化特征向量Λ＊。

第三步：根据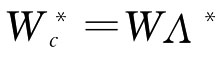并进行归一化处理，求出后得归一化的最优组合赋权向量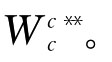

第四步：计算第i个数字图书馆评价方案S_i的多指标综合评价值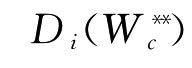，i＝1，2，…，m，并根据各数字图书馆评价方案多指标综合评价值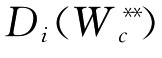的大小对多指标评价问题进行排序，作出科学的分析。

四、最优组合赋权的数字图书馆评价方法的实例分析

设利用层次分析法确定四个指标的权系数分别为：

前已指出层次分析法属于主观赋权法，而熵值法属于客观赋权法。显然两种赋权法所得的四个指标的权系数结果是不一致的。为了综合这两种赋权方法的特点，可考虑如下最优组合赋权法：

设W₁＝（W₁W₂W₃W₄）^T＝（0.4029 0.0562 0.4615 0.0794）^T表示熵值法计算出四个指标的权系数向量值；

设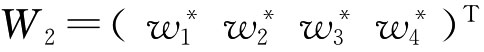＝（0.48 0.24 0.13 0.15）^T表示层次分析法计算出四个指标的权系数向量值；

设组合权向量为W_c＝（W_c1W_c2W_c3W_c4）^T，令：

W_c＝θ₁W1＋θ₂W₂

其中θ₁，θ₂为组合权系数向量的线性表出系数。θ₁，θ₂≥0，且满足单位化约束条件: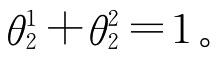

由于不同的指标往往具有不同的量纲和量纲单位，为了消除它们带来的不可公度性，在数字图书馆评价之前首先应将评价矩阵C值作无量纲化处理。

设规范化的评价矩阵B＝（b_ij）_6×4为：令分块矩阵W＝（W₁，W₂），W实际上为4×2的矩阵。即：

Θ＝（θ₁，θ₂）^T，Θ为组合权系数向量的线性表出系数组成的2维列向量。此时W_c可表为矩阵形式：

W_c＝WΘ

由组合赋权系数向量Wc计算而得的第i种数字图书馆方案的多指标综合评价值可表示为：

一般而言，D_i（W_c）总是愈大愈好，D_i（W_c）愈大表示第i数字图书馆评价方案愈优。但是在数字图书馆评价中，如果各指标的权系数确定不当，会致使各种数字图书馆方案的综合评价值D_i（W_c）（i＝1，2，3，4，5，6）互相差别很小，这样将不利于数字图书馆评价。所以选择组合赋权系数向量W_c的一个基本思想是使各种数字图书馆方案的综合评价值D_i（W_c）（i＝1，2，3，4，5，6）尽可能分散，越分散越有利于数字图书馆评价。可采用各种数字图书馆方案的综合评价值的离差平方和作为其分散程度的度量。为此定义第i₁种数字图书馆方案综合评价值D_i1（W_c）和第i₂种数字图书馆方案综合评价值D_i2（W_c）的离差为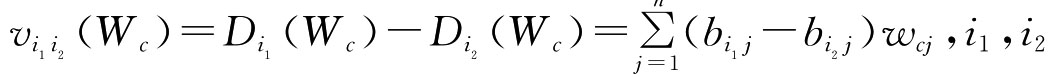：＝1，2，3，4，5，6

设v_i（W_c）表示第i种数字图书馆方案与其他各种数字图书馆方案综合评价值的离差平方和，则有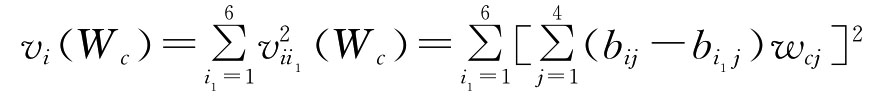：i＝1，2，3，4，5，6

根据前述的选择组合赋权系数向量W_c的基本思想，应该使6种数字图书馆方案总的离差平方和达到最大，这样有利于数字图书馆评价。于是可构造如下目标函数：

若令4×4阶矩阵A＝（a_ij）_4×4，其中第m行第n列元素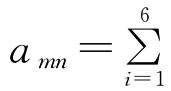，m，n＝1，2，3，4。

经过计算得：

显然A为4阶对称方阵且A为非负定矩阵。则目标函数F（W_c）可表为：

F（W_c）＝AW_c

其中W_c＝（W_c1，W_c2，W_c3，W_c4）^T为组合赋权系数向量。

要想求出组合赋权系数向量W_c，只要求出组合权系数的线性表出系数向量Θ就行了。既然W_c为Θ的函数，从而目标函数F（W_c）也为Θ的函数，此时F（W_c）可记为F（Θ）。于是6种数字图书馆方案总的离差平方和的最优组合赋权方法即为如下最优化问题：

maxF（Θ）＝Θ^TW^TAWΘ

该最优化问题可简化为如下无约束优化问题：

根据矩阵理论，F₁（Θ）是线性表出系数向量Θ的Rayleigh商。显然W^TAW是对称矩阵，则由Rayleigh商性质知，F₁（Θ）存在最大值。

设λ_max为矩阵W^TAW的最大特征根，Θ^＊为矩阵W^TAW的最大特征根所对应的单位化特征向量，则F₁（Θ）最大值为λ_max，且Θ^＊为上式的最优解。

由W和A计算对称矩阵W^TAW为：

从而计算出W^TAW的最大特征根λmax＝4.6824，它所对应的单位化特征向量

Θ^＊＝［0.4654 0.8851］^T

由于传统的加权向量一般都是满足归一化约束条件，因此为了与人们的习惯用法保持一致，还需要对Θ＊进行归一化处理得：

Θ^＊＊＝［0.3446　0.6554］^T

根据Wc＝WΘ＊＊算出数字图书馆方案4种评价指标的组合赋权系数为：

W_c＝0.3446 W1＋0.6554 W₂＝（0.4534，0.1767，0.2442，0.1257）^T

将W_c代入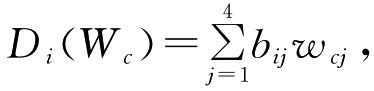，i＝1，2，3，4，5，6，分别计算6种数字图书馆方案的多指标综合评价值为：

计算结果表明：

第1种数字图书馆方案＞第4种数字图书馆方案＞第2种数字图书馆方案＞第3种数字图书馆方案＞第5种数字图书馆方案＞第6种数字图书馆方案

其中“＞”表示优于。

综上所述，本节给出了数字图书馆评价的最优组合赋权方法，它综合了各种赋权方法的特点，通过一个最优化数学模型求出组合赋权系数。在计算机高度发达的今天，该最优化模型的求解是不成问题的。可采用MATLAB^［26］计算软件求解最优化模型。因此，最优组合赋权方法可操作性较强，在数字图书馆评价领域中具有重要的推广应用价值。