咨询项目中引力模型的成功应用

引力模型在咨询项目中的初步应用

沈源

一、引力模型简介

1687年牛顿提出的万有引力定律，成为近代科学发展的基石，既任何物体之间都有相互吸引力，这个力的大小与各个物体的质量（分别为M₁和M₂）成正比，而与它们之间的距离（r）的平方成反比。万有引力定律的公式为：F=(GM₁M₂)/r²

二、社会科学中的引力模型

物理学与经济学等社会科学的联系是非常紧密的，早在19世纪末，英国就将引力模型用于人口统计分析；在20世纪30年代，美国学者赖利（W.J.Reilly）将引力模型推广应用到社会科学研究的各个领域，特别是经济学分析和经济地理学研究，成为研究空间相互作用的核心工具之一。

引力模型非常便于实证分析，经常被经济学家和咨询工作者所使用，进行市场分析与投资决策。

物理学中引力模型的理论依据是牛顿万有引力定律，社会科学中引力模型的理论依据则是距离衰减原理。所谓距离衰减原理，是指各经济现象之间存在的相互作用，其相互作用将会随着相互之间距离的增加而减少。社会科学中引力模型的一般表现形式可分为双点模型和多点模型：

双点模型：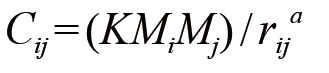

其中，C_ij表示j点对i引力的大小，M_i、M_j分别表示两点的“质量”（可以用人口、面积、收入等表示），r_ij表示两点间的距离（可以用路程、时间等表示），K、a为系数。

多点模型：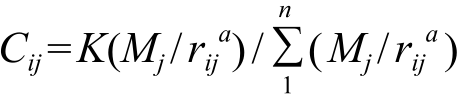

多点模型的含义与单点模型的含义基本相同。此外，多点模型两点之间的距离有时可以使用向量的形式来表示。

三、引力模型在咨询领域中的应用

引力模型在市场分析、国际贸易、区域经济等众多咨询领域中有着广泛的应用，引力模型研究的结论常被作为投资决策、区域规划、项目评估等的重要依据。

市场分析领域——市场分析是引力模型最广泛的应用领域之一，常用于研究市场位置、人流量、规模、定位等，与消费者距离、交通、收入、消费习惯等之间的关系，市场包括零售市场、房地产市场、旅游市场等。

国际贸易领域——应用领域包括国际贸易、边境贸易、区域贸易、国际物流等方面，例如进出口量预测、贸易顺差与逆差研究、地区贸易合作、贸易自由化、吸引外商投资、消费者偏好分析等实证研究。

区域经济领域——用于研究不同城市、不同区域空间之间的相互作用，包括城市规模和城市之间距离对交通、市政、就业、商业、工业发展等的影响，以及预测城市经济圈的最佳规模等。

四、零售引力模型案例分析

本章节通过一个市场分析领域案例，来介绍引力模型在商业人流预测咨询项目中的实际应用。(www.xing528.com)

零售引力模型——商业圈的主要零售商业吸引的客流量，与零售商业的规模成正比，与到达该零售商业的距离成反比。该模型是传统引力模型的衍生应用，是目前最为常用的预测零售商业人流及规模的方法之一，能够根据常住人口数量、零售商业规模、常住人口与零售商业的距离，有效测算出多个零售商业区之间的相互作用。其计算公式为：

式中　P(C_ij)—居住在该地块i的居民在零售中心j进行购物的概率；

　S_j—零售中心j的规模，用平方米表示；

　T_ij—居住在地区i的居民到零售中心j的距离；

　n—整个区域内零售中心的数量；

　a—反映不同居民出行时间作用的系数，一般情况下取2。

某城市有3个零售商业中心，分别为A商业中心（20万平方米）、B商业中心（12万平方米）和C商业中心（10万平方米），另有3个居民点，分别为D居民点（3万人）、E居民点（5万人）和F居民点（6万人）。商业中心和居民点两者之间的距离（以时间表示）详见表和下图。

表　某城市商业中心至居民点的距离

图　某城市商业中心和居民点的分布

根据零售引力模型，D点居民到A商业中心购物的概率P(C_DA)为40.61%，计算方法如下：

同理可得，

通过计算，可以求得A商业中心吸引的人流量为5.42万人；

同理可得，B商业中心吸引的人流量为3.34万人；

C商业中心吸引的人流量为5.24万人；

以上是某城市3个商业中心吸引人流量的初步预测模型，如果能够得知消费者收入、年龄结构和嗜好，以及不同商业中心的商业业态和市场定位等数据，还可以使用零售引力模型进行较为深入的分领域商业业态客流预测。

五、结论

由万有引力定律发展而来的引力模型是非常经典的实证分析工具，目前决策者、咨询人员、经济学家等社会科学工作者使用较多，用于分析和预测市场、投资、贸易、区域经济等之间的关系。实践证明，在基础数据准确、模型构建合理的前提下，引力模型分析、预测结果相对比较准确，且模型的构建和计算较为简便。

但是引力模型的一大缺陷在于其理论依据相对缺乏，在各种参数（例如K，a等参数）的选取上还存在一定的主观性和不确定性。在各类咨询项目中应用引力模型需要考虑相关影响因素，同时配合使用其他的咨询方法和模型，对引力模型进行理论和实践的验证，以得到最佳的咨询成果。