逻辑思维教程：简单命题负命题讲解

第一节　简单命题的负命题

负命题是通过否定一个命题而得到的新命题。我们称被否定的命题为原命题，否定原命题所得到的命题为负命题。

一、简单命题中A命题的负命题

在简单命题中，如果A命题为原命题，则它的负命题为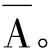从简单命题中的逻辑对当关系中可知，A假，O必真；也就是说A命题的负命题，等值于O命题。可证明如下：

如果A真，则E假，O假，则A为假；

如果真，则A假；如果A假，则E真假不定，而O必真；

如果假，则A真；如果A真，则E假，而O必假。

所以A的负命题等值于O命题。它可以表述为以下几种情况：

第一，并非所有S都是P。

第二，S不都是P。

第三，不能说所有S是P。

二、简单命题中E命题的负命题

在简单命题中，E命题为原命题，它的负命题为从逻辑对当方阵中证明可知E假，I必真；也就是说，E命题的负命题，等值于I命题。它可以表述为以下几种情况：

第一，并非所有S都不是P。(www.xing528.com)

第二，S不都不是P。

第三，不能说所有S不是P。

三、简单命题中I命题的负命题

如果I命题为原命题，它的负命题则为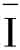，从对当方阵中证明可知，I假E必真；也就是说，I命题的负命题，等值于E命题。它可以表述为以下几种情况：

第一，并非有（些）S是P。

第二，没有S是P。

第三，不能说有（些）S是P。

四、简单命题中O命题的负命题

如果O命题为原命题，它的负命题为可以读作“非O”或“O假”。从对当方阵中证明可知，O假，A必真；也就是说，O命题的负命题，等值于A命题。它的语言表现形式有：

第一，并非有（些）S不是P。

第二，没有（些）S不是P。

第三，不能说有（些）S不是P。