论向量在几何研究中的优势
杨在荣 屈红萍
摘 要:几何代数化已经成为现代几何研究的发展方向,向量是几何代数化的重要组成部分。本文论述了向量在几何研究中四个方面的优势:向量运算具有简洁性,向量解几何问题的基本法则简练明朗,用向量研究几何可以实现形象思维与抽象思维的有机结合,向量拓宽了研究和解决几何问题的思维空间。
关键词:向量 几何 研究 优势
向量的学习始于物理,利用力作为向量的模型,用实验的方法研究求两力合力的平行四边形法则,而后又用位移作为向量的模型得到了向量加法的三角形法则。在数学中,长期以来向量仅作为空间解析几何的基础知识来学习,甚至在20世纪80年代向量都还披着神秘的面纱。近几年来,向量在数学中的应用得到重视和发展,已经涉及更为广泛的其他数学知识和学科,特别是几何。几何代数化已经成为现代几何研究的发展方向,向量具有几何与代数双重属性,是几何代数化的重要组成部分,在几何研究中体现出了它特有的优势。
一、向量运算的简洁性
众所周知,几何命题的解证难就难在灵活性大、技巧性强,常常需要灵机一动。特别是当人们发现了行星绕地球旋转的轨道为椭圆、抛出去的石子经过的路线为抛物线之后,仅用综合几何的方法来研究几何是不行了。以笛卡儿为代表所创建的坐标几何,实现了几何代数化,使几何能够用代数的方法来研究。但是,人们同时也感到运算的烦琐,而向量不仅能够实现几何代数化,而且在“以算代证”过程中具有运算简洁的优势。
例1(三角形重心定理):三角形的三条中线相交于一点,并且这点分各中线的线段比为2∶1。
图1
证明:
设中线BE和CF相交于点G,D为BC的中点(图1),则
由平面向量基本定理得:
所以A、G、D共线,于是三中线AD、BE、CF共线,且点G分三中线线段比为2∶1。
例2:已知E和F分别为平行四边形ABCD的边AD和BC上的点,且AE= BF,G是AF和BE的交点,H是CE和DF的交点。求证: GH//BC,GH=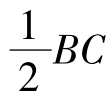 。
。
图2
证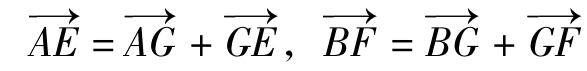 明:
明: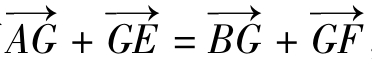 ,从而,由平面向量基本定理得
,从而,由平面向量基本定理得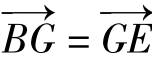 ,G为BE中点。同理,H为CE的中点,所以,GH//BC,GH=
,G为BE中点。同理,H为CE的中点,所以,GH//BC,GH=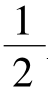 BC。
BC。
二、向量法解几何题的基本法则简练明朗
应用综合几何的方法解几何问题要用到许多公理和定理,而用向量解几何问题的基本法则仅有4条,这从根本上体现了向量法简练明朗的优势。→→
法则1:首尾相接法则。即向量加法的三角形法则─AB+─
BC=─A→C,推广到有限多个向量时即为向量加法的多边形法则。
法则2:数乘向量的意义和运算律→。→ 3::─e,─e
法则平面向量基本定理设12是平面上两个不共线向量,则平面上任意向量→a都可以表示成→a=λ→─e+μ→─e,且λ,12μ由→a和→─e1,→─e2唯一确定。
从平面向量基本定理可以立即得到如下推论:如果→a+→ b=→ c+→ d,且→a和→c共线,→b和→d共线,但→a和→b不共线,那么→a=→c,→b=→ d。
法则4:向量内积的意义和运算律。特别是两向量垂直的充要条件,即向量→a和→b垂直的充要条件为→a·→b=0。
法则1和法则3主要应用于涉及包含关系和位置关系等仿射性质,涉及的几何量只是在平行或共线的线段比的范围。
例3(塞瓦定理):如图3,AD、BE相交于G,若CG的延长线交AB于F,则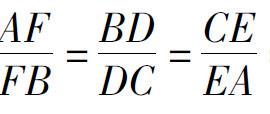 = 1。
= 1。
证明:
设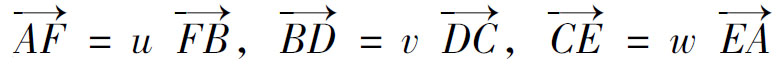 则
则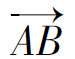 =(1+
=(1+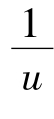 )
)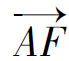 。
。
图3
整理得:
由平面向量基本定理得:
整理得:
从而u(1+ v)=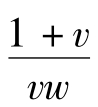
所以uvw= 1
如果涉及度量几何,即涉及长度、角度大小及垂直,或者涉及不平行线段的比值等,则用向量的模和法则4解决。(https://www.xing528.com)
例4(射影定理):在△ABC中,AB⊥BC,BD⊥AC。求证: AB2=AD·AC,BC2=CD·CA,BD2=DA·DC(图4)。
图4
证明:
同理
例5:在正三角形ABC中,D、E分别为AB、BC的三等分点,AE,CD相交于点P。求证: BP⊥DC(图5)。
图5
证明:
从而得:
由平面向量基本定理得:
即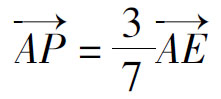
从而得:
所以BP⊥DC。
用向量解几何问题时,向量形式的定比分点公式是一个重要工具,如图6中: P1P=λPP2(λ≠-1),则OP=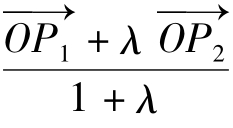 。
。
图6
例6(梅涅劳斯定理):设直线l与△ABC的三边AB、BC、CA(或延长线)分别交于D、E、F且不过三角形的顶点,则 =-1(图7)。
=-1(图7)。
图7
证明:
三、用向量研究几何可以实现形象思维与抽象思维的有机结合
几何图形直观形象,正如笛卡儿所说,“没有什么比几何图形更容易印入人的脑际了”;代数抽象严谨。向量具有几何与代数的双重身份,用向量可以实现形象思维与抽象思维的有机结合。这在所有用向量研究几何问题的过程中都得到体现。在此,仅举一例加以说明。
例7:用向量法证明余弦定理。
证明:
在△ABC中,设─B→C=→ a,─C→A=→ b,─A→B=→ c,且设→a= a,→b= b,→c= c,则→a+→ b+→ c=0,→a=-(→b+→ c),从而→a2=→ b2+→ c2+ 2→b·→c=→ b2+→ c2+ 2→ b→ccos(π-A)。即a2= b2+ c2-2bc cos A。
再如,在用坐标法研究几何问题时,经常先通过向量,得出向量形式的结果后再转化成坐标形式,这实际上也是向量的这个优势的体现。
四、向量拓宽了研究和解决几何问题的思维空间
向量代数提供了一种有别于数域的新的代数结构,它不仅揭示了知识之间的联系,而且拓宽了研究和解决几何问题的思维空间。
例8: P为⊙O: x2+ y2=4上任意一点,l为过P的切线,A(-1,0),B(1,0),A与A'关于l对称,求A'B的最大值(图8)。
图8
解:
设AA'交l于Q,连接OP、OQ,则OQ//A'B且A'B= 2OQ,又AQ⊥l,OP⊥l,所以AQ//OP。设A→Q=λ─O→P(λ>0),则─P→Q=P→O+─O→A+─A→Q= ─P→O+─O→A+λ─O→P=(λ-1) ─O→P+─O→A,又─O→P·─P→Q=0,即─O→P·[(λ-1) ─O→P+─O→A]=─O→P2(λ-1)+─O→P·─O→A= 4(λ-1)+ ─O→P·─O→A= 0,从而─O→P·─O→A= 4(1-λ),又─O→Q=─O→A+─A→Q=─O→A+λ─O→P,所以─O→Q2=─O→A2+λ─O→P2+2λ─O→P·─O→A= 1+ 4λ2+8λ(1-λ)=-4(λ-1)2+5。
所以,当λ=1时,OQ最大值为√5,即A'B的最大值为2√ 5。
参考文献:
[1]张景中,彭翕成.论向量法解几何问题的基本思路[J].数学教学,2008(1).
[2]陈振宣.向量面面观[J].数学教学,2008(5).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




