高校学生考试作弊行为的博弈研究：探索与创新

高校学生考试作弊行为的博弈研究

屈红萍　杨在荣

摘　要:杜绝和减少高校学生考试作弊是高校教学环节的重要措施。本文运用博弈论来分析考试作弊现象，建立作弊者与监督者的混合战略博弈模型，并对模型进行分析研究，得出一些有益的结论，进一步提出有效防止学生作弊行为产生的一些对策。

关键词:博弈论　作弊　监考　混合策略

在高校教学过程中，考试是一个重要的环节，是检查教师教学效果、评定学生学业水平的重要指标，且能同时调动教与学两个方面的积极性。然而，在高校名目繁多的考试中，学生的作弊行为仍较为突出，并且呈现考试作弊人数增多、作弊手段多样化等特点。大学生考试作弊已成为高校中诸多不良现象之一。诚然，学生作弊有其内在原因，另一方面，学生作弊的行为又与考场监考教师的态度认真与否紧密相连。对此，本文将建立学生与监考教师的博弈模型，对考试作弊行为产生的原因进行定量分析，以期找到相应的解决方法和对策。

一、模型的假设和建立

博弈论研究的对象是理性的行动者或参与者如何选择策略或如何作出行动的决定。博弈论认为，每一个完整的博弈过程一般由下列四个基本要素组成。

第一，参与人(Players)。指的是一个博弈中的决策主体，每个参与人都是一个决策者。这些决策者彼此之间是对手，对手可以是个人、团体、企业组织，也可以是国家。假设每一个参与人都是理性的，都根据实现自身利益最大化或自身损失最小化的原则进行决策，博弈中的参与人数大于或等于2。当有两个参与人时，称为两人博弈;当有n个参与人时(n＞2)，称为多人博弈。

第二，策略(Strategies)。它是指参与人的行为取舍、经济活动水平等可供选择行动的范围。在博弈中，每个参与人可供选择的策略数可以是有限的，也可以是无限的。有限策略的博弈称为有限博弈，构成了博弈论研究的主体。在有限博弈中，若参与人在决策过程中，若干可选策略中各个策略彼此相互独立时，称为单纯策略;反之，若参与人按某种概率分布对可选策略进行组合，称之为混合策略。

第三，支付或效用(Payoffs)。它是参与人从博弈中获得的效用程度，是所有参与人策略或行动的函数，是每个参与人真正关心的核心问题。

第四，均衡点(Equilibrium)。它也是所有参与人的最优策略或行动的组合，在这一点上，假设其他参与人不变换策略，任何单个参与人不能以单方面变换策略来提高他的效用程度。

按照博弈论的假设，我们建立监考博弈模型。监考博弈模型的参与人为学生与监考教师。监考教师有两种策略可以选择:认真监考和监考不力;学生也有两种策略可以选择:作弊和不作弊。作为理性人，他们都有自身利益最大化的行为理性，由于现实中两者各自利益上的权衡和决策，使得双方的得益支付矩阵如下表:

其中，F是学生作弊被抓住的惩罚，W是教师认真监考获得的收益(如工作量补贴、表扬等)，R是不认真监考的收益(W＞R)，C是教师付出的成本(如制作学生信息卡、提前清场、检查证件、认真监考)，Y是学生作弊成功得到的收益，F、W、C、Y、R均大于零，W－C＞R。

二、模型的研究与分析

根据上图中收益数字下所画短线和箭头的方向可以知道，这个博弈不存在纯策略纳什均衡。因为假设学生选择“作弊”的策略，那么对监考老师来说最好的策略选择是“认真”，这样可以使作弊学生受到惩罚，但当监考教师选择“认真”时，学生的正确策略就是“不作弊”而不是“作弊”，既然学生选择“不作弊”，当然监考教师选择“不认真”比较合算，而监考教师“不认真”时，学生就会选择“作弊”策略，这样可以获得更大的收益……这样重复下去，永远不可能停止，无论从哪里开始都是一样的。因此这个完全信息静态博弈在一次性博弈中没有自动实现的均衡性策略组合，更无法预测到博弈的最后结果。

因此，该博弈中两博弈方的决策原则是不能让对方预先知道或猜到自己的策略，应该以随机的方式选择策略，并且随机选择两种策略的概率，不能让对方有可乘之机。这样，师生双方必然在各自利益最大化的原则下寻求混合策略意义上的纳什均衡。在这种情况下，我们可以求解混合策略纳什均衡。

假设监考教师以p概率选择“认真”和1－p概率选择“不认真”，学生以q概率选择“作弊”和以1－q概率选择“不作弊”，那么根据上述决策原则，学生选择“作弊”和“不作弊”的概率为q和1－q时，一定要使监考教师选择“认真”的期望收益和“不认真”的期望收益相等，即(W－C) q+(－C)(1－q)=Rq+R(1－q)，简化可得q=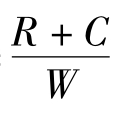，这就是学生作弊的最优概率。同理，监考教师选择“认真”和“不认真”的概率为p和1－p时，也应使学生选择“作弊”的期望收益和选择“不作弊”的期望收益相等，即－Fp+ Y(1－p)= 0×p+ 0×(1－p)，简化得p=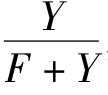，这也是监考教师认真监考的最优概率。当学生以(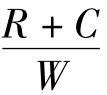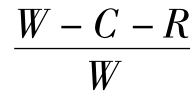，)的概率随机选择“作弊”和“不作弊”，监考教师以(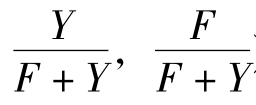)的概率随机选择“认真”和“不认真”时，由于谁都无法通过单独改变自己随机选择的概率分布改善自己的期望收益，因此这个混合策略组合是稳定的。这就是本博弈唯一的混合策略纳什均衡。

对于此博弈的混合策略纳什均衡，我们也可以借助于形象的图形来解释。我们不妨先讨论学生采取“作弊”和“不作弊”两种策略的概率分布下监考教师“认真”的期望收益(见图1)。

图1

横轴表示学生选择“作弊”策略的概率q_t，它分布在0到1之间，“不作弊”的概率则等于1－q_t，纵轴则反映对应于学生“作弊”的不同概率，监考教师选择“认真”策略的期望收益。图1中从－C到W－C连线的纵坐标就是在横坐标对应学生“作弊”概率下，监考教师选择“认真”的期望收益。

根据博弈论的知识容易证明该线与横轴的交点q_t'就是学生选择“作弊”的最优概率水平，选择“不作弊”的最优概率为1－q_t'。

假设学生的“作弊”概率大于q_t'，此时监考教师“认真”策略的期望收益大于0，因此监考教师肯定百分之百选择“认真”策略，这样学生“作弊”一次就逮到一次，因此对学生来说大于q_t'的“作弊”概率是不可取的。反过来，如果学生“作弊”的概率小于q_t'，则监考教师“认真”策略的期望收益小于0，“不认真”策略的期望收益大于0，因此监考教师选择“不认真”的策略是合算的，此时即使学生提高“作弊”的概率，只要不大于q_t'，监考教师都会选择“不认真”的策略。因此，学生不必担心会被处罚，由于学生在保证不被处罚的前提下“作弊”的概率越大收益就越大，因此他会使“作弊”的概率趋向于q_t'，均衡点是学生以概率q_t'和1－q_t'分别选择“作弊”和“不作弊”。此时监考教师“认真”和“不认真”的期望收益都等于0，选择策略“认真”和“不认真”的混合策略的期望收益都是相同的。(www.xing528.com)

不过，事实上，为了让学生没有可乘之机，监考教师也必须选择特定概率分布的混合策略。下面以监考教师采取“认真”和“不认真”的混合策略概率分布用同样的方法来分析学生“作弊”的期望收益。

图2

由图2可知，图中q_t'和1－q_t'是监考教师的最佳概率选择。

在学生和监考老师的博弈中，学生分别以概率q_t'和1－q_t'随机选择“作弊”与“不作弊”，监考老师分别以概率q_t'和1－q_t'随机选择“认真”与“不认真”时，双方都不能通过改变策略或概率改善自己的期望收益，因此构成混合策略纳什均衡，这也是该博弈唯一的纳什均衡。

三、结论与对策

通过对上述博弈的分析，我们可以针对博弈的双方参与人从两个方面来分析对学生作弊现象的防治。

一方面，加大对认真监考的老师的奖励力度，即W增大，相当于图1中W－C向上移动到W'－C，如果学生混合策略中的概率分布不变，此时监考老师“认真”的期望收益变为正值，监考老师肯定会选择“认真”。监考老师“认真”，学生只能减少“作弊”的概率，直到将q_t'下降到q_t″，此时监考老师又会恢复混合策略，达到新的混合策略均衡。同样，由q= R+C可看

W出，监考教师认真与否和他的监考收益W与劳动成本C有关，W越大，监考教师的积极性越高，学生选择作弊的概率也就越小。这就是说，加大对监考老师的奖励力度在短期中的效果是使老师真正认真，但在长期中并不能使监考老师更认真，加大奖励力度在长期的真正效果恰恰是会降低学生作弊的概率。

同样，我们讨论加重对作弊学生的惩罚力度。加重对作弊学生的惩罚意味着－F增大到－F'，如果监考老师策略中的概率分布不变，学生“作弊”的期望收益变为负值，学生肯定会选择“不作弊”。但是在长期中，学生“不作弊”会使监考老师更多地选择“不认真”，最终“认真”的概率从p'_t下降到p″_t，学生又会恢复混合策略，达到新的混合策略均衡。可见，加重对作弊学生的惩罚短期内是使学生减少作弊，但长期来说实际是使监考老师更不认真。

从以上博弈分析可以看出，高校学生考试作弊屡禁不止是内外因综合作用的结果。从内因上看，当前，许多高校中综合测评的排名、奖学金的发放、三好生的评选、竞选学生干部和入党等无不与考试成绩挂钩，而作弊具有明显的收益，作弊能提高名次、分数，并由此获得奖学金、评优推先和入党等优势。在个人利益最大化的驱使下，学生会选择自己认为是最好的策略(作弊)。从外因来讲，在监督、惩罚力度大小、作弊风险的权衡下，选择是否作弊。因此，如何从外因方面采取对策杜绝学生的作弊行为也显得尤为重要。综上分析，我们可以从以下几方面进一步对学生作弊形成约束。

第一，加大对学生作弊的惩罚力度。如果对作弊行为的惩罚足够严厉，使学生在教师原来的混合策略下作弊的收益变为负值，学生采取作弊行为时将三思而行。由于惩罚力度加大，对学生的作弊动机约束力加强，从而能降低作弊的概率。目前有不少高校在考试管理中都有相关的一些规定，比如取消一切评优资格，给予留校察看处分、记过直至开除等等。

第二，加大监考老师的监考力度。在对学生作弊惩罚F既定的情况下，学生作弊行为的多少取决于监考的力度。因为如果监考老师不负责任，对作弊行为睁一只眼闭一只眼，即便学校对作弊的惩罚力度足够大，对学生只是不可置信的威胁。只有进一步加大监考力度，才能使严惩成为一种可信的威胁。监考力度与监考老师的责任心、积极性是密切相关的。从降低监考老师的劳动成本C和提高对老师的奖励W入手，可以提高监考老师的责任心和积极性。只有激励没有惩罚是不行的。高校应该对监考老师不负责任的行为进行约束，比如通过巡考人员的监督和学生的检举，若发现监考老师有不负责任的行为要进行一定的处罚。

第三，从上面的博弈分析，可看到加大对监考教师的奖励力度及加重对学生作弊的处罚在短时期内能有效减少学生的作弊行为，但并不是长久之计。作为高校教育工作者，应该在平时的教书育人过程中，紧密结合当代大学生的思想行为，给予学生积极的引导，让学生明白，诚实应考可以养成正确的竞争心态、得失观、荣誉观和诚实守信的良好品质，走出校门后才可以从容面对现实社会日益激烈的竞争。对学生加强诚信教育，使其树立正确的考试观。

第四，改革考试方法。对于一些必须进行笔试的课程，可以降低期末考试成绩在总分中的权重，增加平时成绩的权重。这样可以有效防止某些学生平时不学习，期末突击和“临时抱佛脚”的现象，杜绝这些学生怀着侥幸心理企图通过作弊蒙混过关的行为。在考试方式上增加开卷考试的科目，或实行灵活多样的半开卷考试模式，增加平时实践、实验环节的得分比重。

第五，注重考场形象建设。完善考场管理制度，建立执行惩罚制度的保障体系，对作弊者的处理公正、公开，减少各种因素的干扰，树立考场的严明、公正形象。增加巡考监督，完善考场监控手段，增加作弊难度，增大考场监督力度。

参考文献:

［1］张维迎.博弈论与信息经济学［M］.上海:上海三联书店，1996.

［2］谢识予.经济博弈论［M］.上海:复旦大学出版社，1996.

［3］涂志勇.博弈论［M］.北京:北京大学出版社，2009.

［4］饶异.高校学生考试作弊行为分析的新视角［J］.北京邮电大学学报(社会科学版)，2006(4).