全局存在的两捕食趋向食物链捕食模型古典解

带有两捕食趋向的食物链捕食模型古典解的全局存在性

李成林　尹国成

摘　要:本文考察了在留曼边界条件下带有两捕食趋向和Holing－II型反应函数的三种群食物链模型。应用抛物方程Schauder估计及Lp估计，证明了此模型存在唯一全局古典解。

关键词:食物链　古典解　Schauder估计　Lp估计

一、引　言

在捕食过程中，食饵和捕食者除了自由扩散外，空间的临时变化速度取决于食饵的梯度，即食饵趋向( Prey－taxis)。通常假设它与食饵的梯度成正比。在生态现象中，捕食者被食饵吸引。一般来说，食物越丰富，对捕食者的吸引就越大。在文献［13］中，作者对种群运动个体行为的测定证实了这一假设。因此，具有食饵趋向的捕食模型被提出，它能很好地揭示捕食者捕食的行为过程。最近，一些学者、生态家、数学家研究了与生态物种相关的食饵趋向。食物链是种群生态学中常见的现象，也是生态学中研究群体结构的一个中心课题之一。我们将研究食物链中的一基本例型，即三物种食物链，但包括食饵趋向。

在文献［1］中，作者证明了带有一个食饵趋向的捕食—食饵模型弱解的存在唯一性。在文献［4］中，作者把文献［1］的结果推广到一个n×m反应扩散食饵趋向系统。在文献［14］中，作者证明了带一个食饵趋向的捕食—食饵两种群模型古典解的存在唯一性。在这篇文章中，我们考察如下带有两个食饵趋向和Holing－Ⅱ型反应函数的三物种食物链系统:

其中Ω是Rⁿ中的有界区域，光滑边界为aΩ，u₁和u_i(i= 2，3)分别代表捕食者和食饵密度(u₂既是食饵密度，也是捕食者密度)，正常数a，K_i，r_i，m_i，e_i，m_i/c_i，b_i/c_i，m_i/b_i(i=2，3)分别代表捕食者的死亡率，食饵的环境容纳量，食饵增长率，半饱和系数，转化率，一个捕食者抓捕一个食饵所用的时间，操作时间，完成半饱和率所需的食饵密度;捕食者被食饵所吸引，正常数β_i(i= 1，2)记为食饵趋向的敏感性;流β₁ u₁▽u₂和β₂ u₂▽u₃取决于u₂和u₃种群增加的密度，按此方式，捕食者朝向食饵密度较高的地方进行捕食。

虽然在文献［14］中作者证明了带有一个食饵趋向的食饵—捕食两种群模型具有唯一的古典解，但只有一个食饵趋向且是两个种群。在这篇文章中我们所讨论的模型是具有两食饵趋向的三种群模型，种群维数增加，给证明带来了根本性的改变，为完成证明，我们采用文献［5，15］中的技能来证明。

在整篇文章中，我们假设:

当u₁≥u_1m时，β₁= 0;当u₂≥u_2m时，β₂=0.　　　　　　　(1.2)

当u_i≥u_im时，β_i=0(i= 1，2)，这一假设具有确切的生态解释:当捕食者密度在Ω内某点达到临界值u_im时，捕食者停止捕食，且当u_i≥u_im时食饵趋向系数β_i为0。

在这篇文章中，我们也假设:

其中，0＜α＜1。

这篇文章的主要结论如下:

定理1.1:假设(1.2)和(1.3)成立，则对AT＞0，系统(1.1)存在唯一解U=(u₁，u₂，u₃)∈C^2+α，1+α(Q_T)，且对Ax∈Ω及t＞0有

u₁(x，t)≥0，u₂(x，t)≥0，0≤u₃(x，t)≤K₃.

H.Amann在文献［16，17，18］中已证明了包括系统(1.1)在内的解的局部存在性，但全局解的存在性仍未证明，因此本文只证明系统(1.1)的解的全局存在性。

二、全局解的存在性

首先我们对系统(1.1)建立先验估计。为方便起见，记与T有关的常数为N，与T无关的常数为N₀。

引理2.1:假设U=(u₁，u₂，u₃)∈C^2，1(Q_T)是系统(1.1)的一个解，那么

u₁(x，t)≥0，u₂(x，t)≥0，0≤u₃(x，t)≤K₃.

证明:由系统(1.1)可得

显然，u₁=0是(2.1)的一个下解，利用最大值原理，可得u₁≥0，类似可得u₂≥0和u₃≥0。

另一方面，由系统(1.1)中的第三个方程可得

由(2.2)知K₃是(2.2)的一个上解。因此有0≤u₃(x，t)≤K₃.

证毕。

引理2.2:假设U=(u₁，u₂，u₃)∈C^2，1(Q_T)是系统(1.1)的一个解，那么对A p＞1，有

‖u₁‖LP(QT)≤N，‖u₂‖LP(QT)≤N，‖u₃‖LP(QT)≤N.

证明:在系统(1.1)的第二个方程两边同乘u₂^p－1(p＞ 1)，在Q_T上积分可得

当u₂≥u_2m时，有

因此有

用Gronwall引理，有

所以，对u₂＜u_2m，有

类似地，有

显然，_Ωu₃(x，t)dxdt≤_ΩK(x，t)dxdt≤N.

证毕。

引理2.3:假设U=(u₁，u₂，u₃)∈C^2，1(Q_T)是系统(1.1)的一个解，那么对A p＞5，有

证明:系统(1.1)的第三个方程可写为－d₃Δu₃－(r₃－r₃u₃/K₃－c₃u₃/(m₃+b₃u₃)) u₃=0.

其中‖r₃－r₃ u₃/K₃－c₃ u₂/(m₃+ b₃ u₃)‖Lp(QT)≤N，由抛物方程L^p估计，有

‖u₃‖Wp2，1(QT)≤N.

应用Sobolev嵌入定理(取p＞5)，有

‖▽u₃‖L∞(QT)≤N.

由系统(1.1)的第二个方程可得

－d₂Δu₂+β₂▽u₂·▽u₃

=－β₂u₂Δu₂+ r₂(1－u₂/K₂) u₂－

(t，x)∈(0，T)×Ω，

= 0

(t，x)∈(0，T)×aΩ，

u₂(0，x)= u₂₀(x)≥0

x∈Ω.

　　　　　　　　　　　　　　　　　　　　　　　(2.3)(www.xing528.com)

其中， ‖Lp(QT)≤N.

‖－β₂u₂Δu₃+ r₂(1－u₂/K₂) u₂－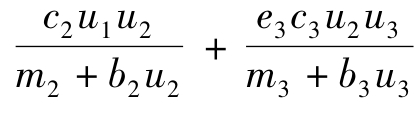

由抛物方程的L^p估计，有

‖u₂‖Wp²，1(QT)≤N.

由Sobolev嵌入定理(取p＞5)，有

‖▽u₂‖L∞(QT)≤N.

类似地，由(1.1)的第一个方程，得

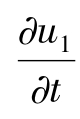－d₁Δu₁+β₁▽u₁·▽u₂=－β₁u₁Δu₂－a+

(t，x)∈(0，T)×Ω，

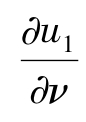= 0

(t，x)∈(0，T)×aΩ，

u₁(0，x)= u₁₀(x)≥0

x∈Ω.

　　　　　　　　　　　　　　　　　　　　　　(2.4)

其中，

‖－β₁u₁Δu₂－a+‖_Lp(QT)≤N.

再由抛物方程的L^p估计可得

‖u₁‖Wp²，1(QT)≤N.

证毕。

引理2.4:假设U=(u₁，u₂，u₃)∈C^2，1(Q_T)是系统(1.1)的一个解，那么对A p＞5，有

‖u₁‖C2+α，1+α/2(QT)≤N，‖u₂‖C2+α，1+α/2(QT)≤N，‖u₃‖C2+α，1+α/2(QT)≤N.

证明:由Sobolev嵌入定理(取p＞5)和引理2.3，得

由(2.5)和系统(1.1)的第三个方程，用Schauder估计得

‖u₃‖C2+α，1+α/2(QT)≤N.

对(2.3)用抛物方程Schauder估计，结合(2.5)可得

‖u₂‖C2+α，1+α/2(QT)≤N.

由(2.5)和(2.4)，用抛物方程用Schauder估计得

‖u₁‖C2+α，1+α/2(QT)≤N.

证毕。

因此，我们可用［5，15］的方法把局部解延拓到A t≥0，即有定理2.1。

定理2.1:假设(1.2)和(1.3)成立，那么对A T＞0，系统(1.1)存在唯一解U=(u₁，u₂，u₃)∈C^{2+α，1+α/2}(Q_T)，且对A x∈Ω和A t＞0，有

u₁(x，t)≥0，u₂(x，t)≥0，0≤u₃(x，t)≤K₃.

参考文献:

［1］B.E.Ainseba，M.Bendahmane，A.Noussair.A reaction－diffusion system modeling predator－prey with prey－taxis［J］．Nonlinear Anal，RWA，2008(9).

［2］H.Amann.Fixed point and nonlinear eigenvalue problems in ordered Banach spaces［J］.SIAM Rev，1976(18).

［3］A.Anderson，M.Chaplain，C.Garcia－Reimbert，C.Vargas.A gradient－driven mathematical model of antiangiogenesis［J］.Math. Comput. Model，2000(32).

［4］M.Bendahmane.Analysis of a reaction－diffusion system modeling predator－prey with prey－taxis［J］.Net. Hetero. Med，2008(3).

［5］A.Friedman，G.Lolas.Analysis of amathematical model of tumor lymphangiogenesis［J］.Math. Models Methods appl. Sci，2005(1).

［6］T. Hillen，K.Painter.Global existence for a parabolic chemotaxismodel with prevention of overcrowding［J］.Advin. Appl. Math，2001(26).

［7］C.S.Holling.Some characteristics of simple types of predation and parasitism［J］.Canadian Entomologist，1959(91).

［8］D.Horstmann，M.Winkler.Boundedness vs. blow－up in a chemotaxis system［J］.J.Differential Equationa，2005(215).

［9］E.F.Keller，L.A.Segel. Initiation of slime mold aggregation viewed as instability［J］.J.Theoret.Biol，1970(26).

［10］W.Ko，K.Ryu. A qualitative study on geneal Gause－type predator－prey models with non－monotonic functional response［J］.Nonlinear Anal，RWA，2009(10).

［11］O.A.Ladyzenskaja，V.A.Solonnikov，N.N.Ural'ceva.Linear and Quasi－Linear Equations of Paraboblic Type［M］．in: Amer. Math. Soc. Transl.，Vol. 23，Providence，RI，1968.

［12］López－Gómez.Positive periodic solutions of Lotka－Volterra reaction－diffusion systems［J］.Differential Integral Equations，1992，5(1).

［13］A.Okubo，H.C.Chiang.Analysis of the kinematics of Anarete pritchardi Kim［M］. col. 10，Springer，Berlin，1980.

［14］Y.Tao.Global existence of classical solution to a predator－prey model with nonlinear prey－taxis［J］.Nonlinear Analysis: Real World Applications(2009)，doi: 10.1016/j. nonrwa.. 05. 005.

［15］Y.Tao，M.Wang.Global solution for a chemotactic－haptotactic model of cancer invasion［J］.Nonlinearity，2008(21).

［16］H. Amann.Dynamic theory of quasilinear parabolic equationsⅠ: Abstact evolution equations［J］.Nonlinear Anal，1988，12(9).

［17］H.Amann.Dynamic theory of quasilinear parabolic equationsⅡ: Reacton－diffusion systems［J］. Differential Integal Equations，1900(3).

［18］H.Amann.Dynamic theory of quasilinear parabolic systems－Ⅲ［J］. Global existence，Math. Z.1989(202).