基金的风险管理：在险价值测量的重要性

早在21世纪初的时候，人们就将在险价值（Value at Risk，VaR）方法的应用从银行领域的监管转到基金领域的监管。简单地说，风险测量的对象即资产收益波动率的大小。在这种情况下，在险价值测量的是组合资产的波动率有多大。

一、什么是在险价值

在险价值概念出现以前，人们使用例如希腊字母等方法来测量衍生品交易组合的风险。金融机构几乎每天都要用这些测度衡量交易头寸所面临的风险。而这些希腊字母的测量包含大量的运算。这些风险测度对于一个交易员来说是至关重要的，但是它们并不能够体现一个金融机构面临的整体风险。因此，我们需要一个方法来度量金融机构整体组合所面临的风险。在这种情况下，在险价值的概念应运而生。

在险价值这个概念的初始，要追溯于丹尼斯·韦瑟斯通（Dennis Weatherstone）就任J·P·摩根主席的时候。他提出了一个问题，奠定了在险价值这个概念的基础：当下一个交易日结束时，我们交易组合的损失会是多少呢？他提出的不是一个风险管理的问题，而是一个风险度量的问题。这个问题所涉及的，不是在一定风险的限制条件下，通过一个什么样的组合头寸，能使银行的交易组合达到利润最大化。它纯粹是个如何测量风险的问题。

对韦瑟斯通提出的问题，有两种不同的方法能够解答：一种解答完全从统计概率的角度，这也是在险价值理论的核心所在；另一种是非量化的回答，这种回答估计了由于一种或一组情景对组合价值所产生的影响。

下面举一个情景分析对组合价值产生影响的例子。我们假设有这样一个头寸为100万美元的股票组合，它是完全根据标准普尔500指数而设计的。为了简单起见，我们认为组合的走势完全同标准普尔500指数吻合，没有任何跟踪误差。我们现在假设有这样一个“糟糕”的一天来临，例如历史上某个特定的一天——1987年10月股市一日大跌22%的情形。如果这样不寻常的一天再度发生，那我们的组合将面临22万美元的损失。

现在的问题是，以1987年10月为基准的风险事件是否是一个合适的选择？有其他更贴切的事件吗？这个问题我们将在之后的压力测试篇章中作详尽的阐述。

与情景分析不同的是，在险价值运用统计概率的方法解答了韦瑟斯通提出的问题，即在“糟糕”的一天，我们的损失将会是多少。在这里，我们运用统计的知识定义了“糟糕”的一天。这样，在给定过去一段时间内，所有可能发生的日收益的概率分布的条件下，只有x%的可能性，损失会超过这个数值（在险价值）。我们在这里定义了“糟糕”的一天，那么发生比这更“糟糕”一天的可能性只有x%。5%在险价值（VaR 5%）表示，在100天的观察期内，明天的日损失等于或超过这个在险价值的可能性只有5%。

二、在险价值定义

在险价值被定义为在一定的置信区间下，一定的时间段内，可能达到的最大风险值。

简单地说，在险价值回答了这样一个问题：在下一个阶段，我们可能发生的损失将会是多少。更精确地说：“在给定的时间段内，给定的概率条件下，组合将面临的损失为多大？”例如，给定时间为一周，概率为1%，在险价值为2 000万美元。我们的估计是，在下周内，组合损失超过2 000万美元的概率为1%。

要计算在险价值，我们需要一个测量单位，一个给定时间段，还有概率。常用的测量单位可以是美元、欧元或其他业务上常用的货币单位。通常使用的概率区间为1%～5%。时间段可以任意选择，通常可以是一天，一周或两周。但前提是，要保证在这个时间段内，组合不发生任何变化。区间长短的选择依赖于资产的流动性和被交易的频繁性。对流动性差的资产，选择的区间通常比较长。

我们还是以前面提到的根据标准普尔500指数建立的100万美元的股票组合为例。假设标准普尔500指数日收益服从均值为0，标准差为100个基本点的正态分布。韦瑟斯通提出的问题在这里就变成预测这个头寸面临的风险有多大。或者更准确地说，在市场明天结束时，预期我们将在这个头寸上损失多少。

要回答这个问题，我们首先回顾一下正态分布的特点。正态分布通常可以用两个参数来描述：μ（均值）和σ（标准差）。

累积分布函数告知我们，X轴上点之间位于标准正态密度函数下的图形面积。例如，在正态分布的条件下，任意一个观察值位于均值与距均值两个标准差之间的概率为47.5%。表2－1中给出了在险价值常用的分位点与其在正态分布条件下对应的值。

表2－1　正态分布函数常用分位数

我们来简单解释一下表2－1。给定一个标准正态分布的随机变量X（均值为0，标准差为1），例如Prob（X＜－1.645）＝5%。换句话说，对于任何一个正态分布的随机变量，它落在距均值1.645个标准差之下的概率为5%。重新回到我们股票组合的例子，标准普尔500指数的日波动被认为是服从均值为0、标准差为100个基本点的正态分布。利用表2－1中给出的正态分布的特性，我们得出，只有5%的可能性，明天标准普尔500指数的损失将大于1.645%（1.645×100基本点）。在例子中，我们假设头寸为100万美元，那么只有5%时间的最低日损失额度将超过16 450美元（0.016 45×100万美元）。换种方法表达，股票组合的VaR 5%＝16 450美元。意味着，只有5%的可能性，标准普尔500指数导向的股票组合的日损失会等于或超过16450美元。另外一种解释为，有95%的可能性，明天我们的组合价值将超过983 550美元（1 000000美元－16 450美元）。运用表2－1，我们还可以计算任何其他的在险价值。例如，VaR 1%＝23 260美元（2.326×0.01×100万美元）。用同样的方法，我们可以计算任何程度风险（置信区间）下的在险价值。

在前面，我们计算了一天的在险价值。有时候，我们想知道一段时间的在险价值，例如，一周、一个月或是一年。这可以通过日在险价值与“开方法则”来实现。法则规定，J天的在险价值等于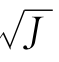×（日在险价值）。由此，一周（5个工作日）的股票组合在险价值VaR 5%可以表示为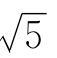×16 450美元＝36 783美元。同样方法，一年的在险价值（250个工作日）的在险价值VaR 5%可以表示为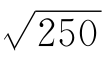×16 450美元＝260 097美元；有5%的可能性，股票组合的损失将超过260097美元（或者说，到年底，有95%的可能性，组合的价值将等于或超过739 903美元）。

在险价值不仅可以通过货币，也可以通过百分比的形式计算出来。目前为止，我们是在通过以货币为单位损失的概率分布来计算在险价值的绝对损失。我们同样可以通过损失百分比的分布来计算在险价值。例如上例中VaR 5%为36 783美元的情况。如果我们不去计算5天在险价值的绝对值，而考虑标准普尔500指数5天标准差的变化，将得到100基本点×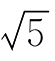＝2.23607%。计算5天的在险价值，为1.645×2.236 07%＝3.678 3%。它表示，有5%的可能性，这个以标准普尔500指数为导向的股票组合将在下周损失3.678 3%。若组合的头寸为100万美元，则意味着损失为36 783美元（100万美元×0.036 783）的在险价值。

作为一个被广泛使用的风险测度，在险价值满足了能够相对容易被估计的特性。那么，它满足其他条件吗？例如，准确度？在险价值的一个假设条件——日收益服从正态分布，导致了这个估计不是十分准确的。估计结果的准确度与它的复杂程度是成正比例的。如果我们想要得到更准确的结果，就需要采用更加复杂的方法。

三、计算在险价值的假设条件

我们在讨论在险价值之前，要明确使在险价值可行的几个假设条件。首先，我们要满足稳定性要求。意思是，收益1%的波动在任何时间段都是一样的。稳定性是为了使在金融数学中普遍使用的假设条件计算简单化。与它相关的假设还有随机游走假设。它认为日收益之间是相互独立的，标准普尔500指数今天损失x个百分点，对明天标准普尔500指数的损益没有任何影响。这样，随机游走可以被定为期望收益为0的假设条件，在股票组合时，情况就是这样。如果日收益均值为0，那么今天的价格水平就是明天价格水平（例如，标准普尔500指数水平）最好的估计。T时刻不包含任何能够预测t＋1时刻价格的信息。

另一个假设就是非负数假设，表示金融资产的价值不能够取负。但是在衍生品问题（例如，远期、期货、互换）上，就打破了这个规则。稳定性要求的假设规定每个单独阶段的假设在整个观测期都有效。

最重要的是分布假设。以简单的股票组合为例，我们假设标准普尔500指数的日收益服从均值为0，标准差为100个基本点的正态分布。我们可以检验这三个假设的准确性。首先均值为0的假设就是值得争议的，因为我们清楚，股票价值，在这里即标准普尔500指数，它的期望收益是正的：无风险利率加市场风险回报。我们来考虑一个均值非0的情况。假设有一种情况，无风险利率为4%，市场风险回报为6%。年总期望收益10%，转换成日收益为4个基本点（1 000基本点/250＝4基本点）。由此而引出，日资产收益服从均值为4个基本点的正态分布，这种假设比0收益的假设更加有说服力。后面我们将讨论，这个假设并不影响我们的在险价值分析。

现在再看日收益标准差为100个基本点的假设。利用平方根的方法，我们可以将年标准差转化成日标准差。在前面的假设中，这意味着标准普尔500指数年标准差为15.8%。“平方根法则”指出，J时间的标准差，可以用一个单位时间的标准差乘以J的平方根。250个工作日，1%的日标准差，利用平方根法则，得到年标准差为15.8%。

最令人质疑的是正态分布的假设。实际数据显示，大部分的证券价格并不服从正态分布。证券价格的分布有尖峰厚尾现象。

四、计算在险价值的方法

（一）分析的方法（或参数方法）

分析的方法，又称参数法，从收集相关影响因子的历史数据开始。它分为以下几个步骤：①将组合中的工具分割成更基本的工具或者是市场影响因子的现金流；②确定市场影响因子的准确分布；③利用统计学的知识计算组合的方差和在险价值。

1.分解金融工具

分析方法的基本思想起源于分解的假设：假设组合中的金融工具可以被分解为一系列依赖于同一个市场影响因子的简单工具。

例如，用这种方法，我们可以将一个两年期的美国国债期票分割成一组零息债券：一个债券为每期的息票，另一个为本金。两份零息债券都依赖于同一个市场影响因子——美国零息债券利率。再稍微复杂一点，一个用外币发行的债券可以被分割为一组外币零息债券和一个外汇现金流。

再举一个欧元债券合约（Euro Bund contract）的例子：假设一个美国组合管理经理，持有一个两年期的欧元债券合约，面值为10万欧元，6%的息票，每年付息。假设欧元的零息债券的利率为4.45%和5.60%，美元同欧元的即期汇率为2∶1。图2－1描述了这只欧元债券合约被分解成零息债券的过程。

图2－1　欧元债券的分解过程

2.确定分布

在分析方法中，人们对市场风险因子的分布作出假设。例如，最广泛使用的假设是摩根的Risk Metrics：假设风险因子呈正态分布。在正态分布的条件下，所有关于风险因子的信息都被归纳为均值、方差和协方差等参数。利用参数方法，我们不需要将所有历史数据都保存下来。

3.计算组合的方差和在险价值

如果组合的所有市场风险因子都呈正态分布，那么这个组合，即所有单个工具的和，也被认为服从正态分布。这表示人们可以用统计学的知识来计算组合的方差（与现代组和优化理论同样的道理）。

其中：

：组合收益的波动率；

：组合中第i个工具的数量，以货币单位计算；

：工具的波动率；

： 第i个同第j个工具的收益之间的相关性。

这个式子给出，用方差来表达的组合风险，不仅是每单个金融工具收益方差的函数，也是每组收益之间相关系数的函数。这意味着，除非组合和收益之间完全正相关（相关系数为1），组合的方差就不是单纯地将各单个资产的方差加总。由于风险分散化的原因，如果单个资产对组合风险的贡献小于单个资产本身的风险，那么组合的风险就小于各个风险的加总。

下面我们再举一个计算国债期货合约的在险价值的实例。在例子中，我们来估计一个于2006年5月24日购入的2006年6月的国债期货合约的在险价值。那天的期货标价为110美元。由于每个期货合约对应的是面值为100 000美元的债券，所以期货价格每变动1美元，头寸价值就会变化1 000美元。通常，在险价值是用收益而不是绝对价格来计算的。收益可以用下面公式得到：

其中，R代表日收益，P为工具的价格。债券期货合约的日收益见表2－2。

表2－2　债券期货合约的日收益

（续表）

为了计算该头寸一天的在险价值，我们需要估计日收益的均值和波动率（以标准差来衡量）。在这里，组合中只有一种工具，我们不需要计算相关系数。如果收益服从正态分布，那么将有95%的收益落在距离均值1.95个标准差之下。98%的收益落在距均值2.33个标准差之下。我们例子中国债期货收益和标准差分别为－0.002 24%和0.605 074%。这表示98%的收益落在－1.41%到1.41%之间，只有1%的收益小于－1.4%。

为了将负的收益（损失）－1.41%转化成货币绝对价值（在这里即美元价值），我们需要找出5月24日的期货价格，即我们要计算的那天的在险价值110美元。通过这个值，我们计算出1%水平上的一天在险价值为1.41%×110×1 000美元＝1 551.00美元。如果计算无误，则表示在观测的100天中，最多有一天的日损失会超过1 551.00美元。

在这里，如果我们觉得一天的持有期太短，一周的持有期更加合适，那么通过前面讲的方法，在假定正态分布的条件下，可以由一天的持有期得到一周持有期的在险价值。在这个例子中，我们得出日收益的标准差为0.605 074%，从而，由5个交易日组成的一周标准差为×0.605 074%。在1%置信区间上，一周的在险价值为3 467.70美元。如果我们持有这个头寸一周，在我们观察的100周中，最多有1周的损失会超过3 467.70美元。

分析方法中的两个假设——正态分布和时间的连续独立性，是我们使用数据处理的核心。在任何置信区间下，我们只关心从历史数据中得出的波动率和相关性，这也是这种方法同历史方法在数据处理上的不同。

波动率随着时间而发生变化吗？

在上例从一年的数据中计算日收益波动率的时候，为简单起见，我们假设一年之中波动率是不发生变化的。然而，实际中，波动率是随着时间发生变化的。比如，最近时间的观察值应该比很久以前的观察值更应当受到重视。例如，如果我们只采用前两个月的收益，而不是一整年的，那么我们计算出的标准差就将是0.651 3%，而不是0.605 074%，由此对应的在险价值就将是1 669.22美元，而不是1 551.00美元。很明显，如果我们采用的分别是1个月、半年或5年的历史数据，得到的结果也会相应有所不同。

在计算波动率的时候，普遍使用的方法是用幂指数的方法将时间加权。这个函数赋予最近的时间以最高的权重。根据最近时间数据的变化，波动率与相关系数也不断发生变化。用幂指数为时间加权来计算收益标准差的公式如下：

λ表示延迟因素，它决定了以往观察值延迟的速度。λ取值越高，最近时间的观察值获得的权重越大。

为了检验在险价值是否对此延迟速度敏感，我们取1%的置信区间，3个不同的延迟参数，持有期为50天，看债券期货收益有何不同。结果见表2－3。

表2－3　不同延迟参数下的债券期货收益

在观察期内，债券期货收益的波动率随着时间发生变化。最近时间所占的权重越小，波动率越高。

（二）历史方法

分析方法的简单与方便决定了它被使用的广泛性，但这并不能说明它是最合适的。Mandelbrot（1963）与Fama（1965）在他们早期的研究中经过实证揭示，资产收益在统计上系统地偏离正态的特性。其他的一些研究也显示，资产收益显示有峰度——集中在均值周围，并且有厚尾现象，并且资产收益有左偏现象。资产损失发生的可能性要比正态假设估计下发生的概率要高。

还是采用我们前面举的债券期货的例子，我们勾画一下2005～2006年日收益的频率图。

在不用假设正态分布的前提下，我们可以通过简单的历史方法来得到在险价值，即通过找出真正历史数据中最低的收益。例如，计算1%概率水平上的在险价值，我们将这些历史日收益排序，找出最低的1%的收益。第一个收益分位点在－1.73%处，表示日在险价值为1.73%×110×1 000美元＝1 903.00美元，比我们前面用参数方法计算的1 551.00美元要多23%。

如果我们要计算其他持有期的在险价值，同时不假设时间连续独立性，就不能在这里简单地将时间开方后乘以日收益。我们必须重新计算新持有期的所有收益，建立新的频率分布，从而找出合适的分位点。

同参数方法相比，历史方法有很多优点。首先，它不需要对波动率和协方差做出任何假设。其次，它不需要对分布本身做出任何假设。一般来说，它无需正态假设。但同时，历史方法的缺点是缺少灵活度。与参数方法不同的是，它不能通过尝试不同的波动率同方差来度量在险价值的敏感性。并且，它要求投资者保存大量真实的历史数据。保持长期的大量历史数据，一方面费用昂贵，另一方面这些数据也可能根本不存在。相反，参数方法只需要分布的参数即可。

（三）模拟方法——从风险因子到在险价值

上文提到的方法，通过估计金融工具本身收益来计算在险价值，并不是经常用到。如果金融机构有一个很大的组合去将所有的工具的历史数据都储存下来，是不可能或不实际的。而且，很多金融工具并不存在历史数据，通常它们都是根据客户进行个性化设计的。在这种情况下，被用来计算在险价值的历史数据就不是由工具本身的收益组成，而是由它们的风险因素，即影响它们价值的工具或是风险因子组成的。例如，对国内债券，风险因子就是本国利率。如果使用外币发行的债券，影响因子就是外国利率和汇率。对一些以股票为基础的衍生品，主要的风险因子就是标准普尔500指数。对于标准普尔500指数的期权，相关的影响因子则是标准普尔500指数的价值，它的波动率，指数的红利，还有无风险利率。

在这些情况下，我们完全可以进一步将纯粹的历史在险价值方法发展成历史模拟方法。在这里，我们不需要观察过去真实组合收益的波动率，只需要利用风险因子的实际值，配合当前组合的成分来进行模拟。通过这种方法，得到模拟的组合收益频率分布，再将它们排序找出分位点，从而确定给定置信区间下的在险价值。

与历史方法一样，历史模拟方法也面临着一个问题，那就是缺乏对不同假设条件进行深入研究的灵活性。然而，不一定需要找出风险因子的历史值，我们就可以通过确定它们所属的分布以及相应的参数，为这些风险因子建模。利用这些分布和参数，我们可以为风险因子做上千种不同的情景假设，并根据每种不同的情景假设，确定组合价值的变化。与历史模拟的方法相同，我们可以通过得到的组合收益找出频率分布图，从而确定在给定置信区间下的在险价值。这种方法通常被称作蒙特卡洛模拟或随机模拟。

作为例子，我们计算一下一个由看涨期权组成的头寸一天的在险价值。看涨期权的持有者被赋予以某个固定的价格买入一种资产的权利，而不是义务。在本例中，我们计算一个针对标准普尔500指数的看涨期权的在险价值。这份期权被以20.90美元的价格于2006年5月28日购入（当天的闭市价格）。这份期权于2006年7月20日到期，赋予持有者以670元美元购入标准普尔500指数的权利。（标准普尔500指数于2006年5月28日的市场价值为674.960 6美元。）

按照下面6个步骤，我们可以找出2006年5月28日当天的在险价值：

（1）计算标准普尔500指数的日收益，并且找出收益正态分布的参数。

（2）通过找出的参数来产生正态分布的随机变量，从而模拟标准普尔500指数一天的收益。

（3）利用模拟出的标准普尔500指数的收益计算出标准普尔500指数的价格。

（4）利用期权定价公式和模拟出的标准普尔500指数为看涨期权定价。

（5）通过模拟出的期权价格为看涨期权计算一天的收益。(www.xing528.com)

（6）找出看涨期权收益分布的参数，计算在险价值。

这个过程的难点所在，是将标准普尔500指数的分布转化成期权价值的分布。在本例中，是使用布莱克－斯克尔斯（Black－Scholes）定价公式来为股票指数定价的。公式如下所示：

其中，d 1和d 2由下式给出：

各符号的含义如下所示：

c：看涨期权的价值；

S：标准普尔500指数的价格；

T－t：距离期权到期日的时间（本例中为53天）；

q：标准普尔500指数的红利（估计为每年2%）；

X：期权的履约价格（本例中为670美元）；

N（x）：标准正态分布的累积分布函数（即变量小于x的概率）；

r：无风险利率，本例中为每年5.5%；

σ：标准普尔500指数的波动率。

为了计算在险价值，我们将收益按分位点排序，并找出位于1%分位点的收益。此处为－0.378 7。2006年5月28日，期权价格为20.90美元。因此，用美元表示的一个合约在险价值为0.378 7×20.90×100美元＝791.48美元。它表示，在100天中，最多只有一天，我们在看涨期权合约上的损失会超过791.48美元。

需要指出的是，本例中在计算波动率的时候，将一年中所有观察的时间的权重都做相等处理。当然，根据观察时间的长短，我们可以将其权重做不同的处理，从而得出看涨期权的在险价值结果也相应有所不同。

（四）在险价值的特性

风险测度的意义在于将以货币单位表示的收益X的分布加总，而得到一个数值，ρ（X）。它有如下4个特性。

（1）单调性（monotonicity）：if X 1≤X 2，ρ（X 1）≥ρ（X 2）

如果组合整体系统价值低于其他组合，那么它所面临的风险一定更大。

（2）平移不变性（translation invariance）：ρ（X＋k）＝ρ（X）－k

如果将组合加入现金k，那么组合的风险也会被降低k。

（3）同质性（homogeneity）：ρ（bX）＝bρ（X）

如果将组合的大小增加k倍，那么风险测度也会增加k倍。这个性质在标准差时使用。

（4）次可加性（subadditivity）：ρ（X 1＋X 2）≤ρ（X 1）＋ρ（X 2）

组合的风险要小于组合中单个资产加总的风险。

（五）组合的在险价值

在前面举出的计算在险价值的实例中，我们讨论的主要是由单个资产组成的组合的在险价值。下面我们来看一个两只股票组合的情况。以此类推，我们可以使用同样的方法来计算由多只股票组成的组合的在险价值。

首先，我们要找出组合收益的波动率。很明显，组合的波动率依赖于其中单个股票收益的波动率。因此，我们首先要计算出这两只股票的波动率。但是两只股票收益之间的关系也发生变化。例如，若两只股票间的协方差为负数，那么若一只股票显示正收益，另一只股票就会产生负收益，以此类推。这样，两只股票间的收益相互制约，从而使组合的波动率低于组合中每只股票的单个收益率。如果再增加一只股票，它与组合原有股票之间不成高正相关，那么通过增加这只股票，又可以降低组合的波动率。为了达到这个效果，我们必须找出各股票收益之间的协方差。只要我们找到股票收益的波动率和协方差，就能确认整个组合的波动率，从而按照前面的方法找出在险价值。

例如我们给股票1，2，3投资了1美元。运用基本的统计知识，组合的日波动率为：波动率（股票1）＋波动率（股票2）＋波动率（股票3）＝2×协方差（股票1，股票2）＋2×协方差（股票1，股票3）＋2×协方差（股票2，股票3）。

如果股票1，2，3日收益之间的波动率为1，我们只需将每只股票波动率的平方根加总，从而得到组合波动率的平方根。但通常情况下，相关系数并不为1，我们就不能简单地将单个资产的波动率加总来得到组合的波动率。在这种情况下，就必须算出各资产间的协方差。

在假定协方差恒等的情况下，我们给每只股票收益相等的权重。如前所述，这并不完全符合事实。例如，我们可以通过GARCH方法来估算随时间而发生变化的协方差。

（六）回溯测试

通过上面的方法，我们得到了组合的在险价值，究竟这个在险价值是否能够准确地预测未来，需要我们来对它进行检验，方法就是用现存的历史数据进行验证，看它的估算是否符合我们历史数据中所示的风险。这个过程我们称其为回溯测试，其含义就是利用历史数据检验模型的精确度。

回溯检验的目的，就是看实际观测到的结果与模型所定义的风险度量的置信水平是否一致，如果模型定义了99%置信度下的风险，那我们就要检验模型的在险价值是否真的备兑了99%的损失。它通常以250天作为回溯测试时间，以确定金融管制机构是否干涉。例如，4个差错以下为绿灯区，不必介入；4～9个差错为黄灯区，金融管制机构可以要求提高巴塞尔资本适足乘数；9个差错以上为红灯区域，金融管制机构会进行调查。

回溯检验使用的方法就是我们在数理统计中常使用的假设检验的方法。总之，回溯测试属于模型验证工作的一部分，通过历史数据与模型结构相比较，来看风险价值是否能够有说服力。

在后面的章节中，我们将对回溯测试进行更详尽的阐述。

（七）情景分析与压力测试

正如前面所阐述，蒙特卡洛随机模拟能够解决非线性衍生品组合在险价值的计算问题，但同样，它也存在不足。我们知道，用过去的波动率去估算未来的波动率，该方法问题重重。同样，进行各种不同的模拟，并要阐明它的分布对今后的计算有影响，也是一件不容易的事情。即便通过大量的模拟也不能够解决这个问题。在这种情况下，情景分析就提供了一种解决办法。

1.相关性假设不再成立

我们假设有一个全球债券组合投资，假设该组合风险分散化得很好，并且利用主权风险收益回报很高，全球债券组合能够获取超额风险调整回报。在为主权债券组合［例如布雷迪债券（Brady Bonds）］的协同运动做历史模拟的时候，使用低相关性。这些相关性体现了由于分散化而产生的低风险。

而且还可以证明，同其他普遍使用的方法一样，利用主权信用风险同样可以低成本地提高收益。然而，历史数据表明，这种假设只有在不发生全球危机的情况下才成立。在危机时期时，会产生传染现象。我们举两个例子。

首先，我们看由保加利亚和菲律宾发行的布雷迪债券收益率间的相关性。简单地说，这两个国家的信用度是毫不相关的。它们从地理位置上讲相隔甚远，影响经济发展的因素也各不相同。事实上，由这两国发行的债券收益的相关性也非常低——大约在0.04。由这两国发行的债券组成的组合几乎不显示普遍的波动率。然而，在1997～1998年的东亚经济危机的时候，它们的相关性徒然从0.04增加到0.84。

第二个例子涉及的是美国政府债券与日本政府债券收益之间的关联。这两只债券在一般时期显示很低的相关性。但它们的相关性也随着时间而发生变化，1990年前估算的相关性为0.20。但1990年夏天到1991年海湾战争期间，它们的相关性增长到0.80。由于油价上涨而引起的通货膨胀的担心导致了全球收益率水平的上升。

通常情况下，人们更需要在危机发生时分散化风险，以免产生极端的损失。波动率和相关性的升高，制造了完全不同的收益产生过程。表2－4给出了几个压力事件的案例，以及有关变量在事件之前和之后相关性的变化。

表2－4　金融危机举例

除了1997～1998年的亚洲金融危机以及1990～1991年的海湾战争，还有其他几个相关性瓦解的例子。

（1）在英国退出ERM期间和之前，英镑/美元汇率和英镑LIBOR；

（2）1994年墨西哥危机时，比索/美元汇率以及比索利率；

（3）1987年股市崩盘期间与之前，高信用度与低信用度债券收益变化。

2.产生可信的压力

我们前面所讨论的相关性假设不再成立，是建立在以协方差矩阵为基础的SMC模拟方法上。采用这种方法来估计在经济正常时期的结果，不能够满足危机时经济状况的特征。危机时，要求我们进一步关心尾部的极值分布。在模拟后，要求看看它的0.01个分位点，以及100 000次的第10个，也是平常的事情。经常有金融机构为了获得一个大的组合的该值，整个周末都在进行随机模拟运算。很不幸的是，这个在给定协方差下计算出的100 000次中的第10个，与10 000个事件中的1件并无关系。以天为单位计算，这10 000个事件中的1件大约40年才发生一次。

3.实践中的压力测试

压力测试已经融入到几乎每个金融机构的风险管理系统。通常的风险报告包含两个部分：一个是以在险价值为基础的风险报告；另一个就是以压力测试为基准的风险报告。以在险价值为基础的分析，包含对整个交易组合的相关风险生成因素的由上而下的全面分析。以压力测试为基准的风险报告采用下面两种方法的一种：①一系列历史压力试验；②分析一组事先假定好的压力情景。在两种情况下，我们都要度量这些情景对整个交易组合产生的影响。

历史压力事件包含例如1987年大崩盘、1990～1991年海湾战争、1994年墨西哥危机、1996年东亚危机和1998年长期资本管理公司（LTCM）的近乎崩溃等事件。另一种选择就是使用预先假设的情景。例如，我们假设如果利率发生200个基本点的极端变化，波动率上升了25%，等等，对组合的价值会产生何种影响。后者是很多机构规定的必须要考虑的因素（例如，储蓄银行就被要求验证收益曲线平移的情况会对机构的资产与负债组合产生何种影响。）

压力测试能够提供很多有价值的信息。针对过去极端事件的分析可以为组合的弱点提供大量有价值的信息。标准情景分析可以提供一些标准因素，例如利率变化，对组合产生的风险有多大。

通常，人们要做期限结构情景分析。如果国内利率发生变化，那么我们关心在利率期限结构发生平移或旋转时，利率风险暴露会对银行组合风险产生什么样的影响。

一般来说，全球利率的变化一般是同时同向的，至少在它们同时有大的变化时，国内债券组合就可能同时产生大的损失。这种效应会导致风险估计的误差：多头与空头的风险会被高估，只有多头的组合风险会被低估。

另一个问题就是所谓的资产等级所属风险。通常说，有些资产等级存在资产等级所属风险。例如，新兴市场债务就面临传染风险即投资主权债务的投资者面临全部损失的情形。另一个例子是房屋抵押债券，在这里，利率风险只是全部风险的一部分。还有其他一些尚未被完全很好理解的风险因素。

从学术的角度出发，有必要将这些风险区分开来，哪些是理性的，哪些是非理性的。由于投资者的“投资情感”或“传染”而导致的同资产等级内的同向运动，我们称其为市场非理性。同时，同样资产等级内的同向运动，也可以由模型等理性因素解释。由于模型对定价产生的误差，可能会影响压力测试的准确性。

值得注意的是，资产所属风险对那些风险分散化不足的金融机构是至关重要的。这些机构应该有能力度量，报告和管理已知风险（例如利率风险），但通常无法度量和管理整个风险暴露。

在给资产定价的时候，整体风险被认为是不重要的。资产定价公式中并未涉及给非系统性风险定价——它只给系统性风险定价（无论是市场风险、利率风险或是其他形式的系统性风险）。然而，对于风险管理者来说，特别是风险分散化不足的资产组合，系统性风险与非系统性风险是同样重要的。

4.压力测试与历史模拟

如前所述，一般压力测试是根据过去的事件来调整压力测试中金融市场的波动率参数。这种方法的弊端是，有可能忽视真正影响金融机构的风险源。另外的选择办法，是建立在历史模拟的构思上。构思的出发点是让数据自己决定，哪种情形更适合“极端压力”。

例如，以一周为观察期，检验过去20年中，所有对交易组合的收益产生影响的风险因素。过去20年的观察期，包含1 040周，也包含那些情景分析常用的大事件。然而，一个固定收益组合比一个股票组合，或是货币组合，更容易经历极端事件。因此，我们必须根据不同的资产，确定不同的观察期。在这种情况下，我们不需要对所有的历史事件作情景分析，我们只需选定一些特定的情景即可。

与历史模拟不同，我们在这里对5%的在险价值，即100个交易日中的第5个，或是1 040个交易周的第52个，并不感兴趣。我们关心的是，给定今天的组合，交易中5个或10个最差的周。这会帮助我们确定组合的真实风险暴露。例如，长期资本管理公司崩溃是一个相关压力事件，数据本身会显露出来。东亚危机是相关的，这会通过它们的极端运动体现出来。

1994～1995年间由于利率下降而导致的再融资，不被作为主要的压力事件。然而对于房地产组合风险，事情就不是这样了。对于一个抵押担保债券（CMO）的持有者，这是个非常关键的因素。

5.资产集中

任何关于风险管理的讨论都离不开分散化这个概念。分散化是一个数学效应，它不是理论。现在的问题是怎样达到分散化。长期资本管理公司（LTCM）认为，不同的交易是由公司不同部门来完成的，这个观点在这里不成立。事实上，有一个对所有交易都产生影响的风险因素，那就是流动性风险。这是一个难以量化或预测的风险。与其他风险因子不同，流动性风险很难被测量。

压力的传染事件很难被预测。更不幸的是，金融市场上发现了一系列导致传染的途径和因素，这个名单变得越来越长。1973～1974年发生的通货膨胀是由1973年10月中东战争引起的。1987年的崩溃没有明显的原因；亚洲金融危机是由于泰国货币贬值引起的；有些观点认为，互联网泡沫是由于2000年的微软事件引起的。

这个问题的唯一解决方案看起来很简单，即通过为指定交易对家风险暴露和单个资产以及资产等级全部面值设定阈值。例如，金融机构常用的办法就是为每个单独的交易对家设定信用风险暴露最大阈值。这个阈值可以是贷款的总额度，或是总面值，或是盯市头寸的函数。通常，这个阈值是交易对家和机构资本的百分比。

这个方法可以说既简单又实用。例如，人们可以说，为盯市暴露设立阈值是可以理解的，但是为债务总额面值设立阈值难以理解。我们举个例子，卖出平值期权与卖出虚值期权。如果我们想固定下盯市的风险敞口，并且通过执行价格进行比较。很明显，虚值期权的面值要大得多，因为它的价值很小。这就是关键点所在。对面值的限制变得有意义，因为它是极端情况下暴露的唯一可能参数。

表2－5中两个看跌期权卖方的例子，就能够说明这个情况：一方卖出在值看跌期权，另一方卖出虚值看跌期权。假设期权到期日为1年，标的资产的波动率为16%，年无风险利率为5%。标的资产的当前值为100。以执行价位100的在值看跌期权的价格为4.08，虚值看跌期权的价格为0.25。

表2－5　理论上压力与头寸阈值

日标准差接近1%，为了简单起见，我们假设标的资产跌2%到98，对应的在险价值为2.5%的在险价值尾端。标的资产跌到98，将使在值期权的损失从4.08增长18%到4.82，虚值期权的损失从0.25增加36%到0.34。很明显，在标的资产同样运动的情况下，虚值期权经历的百分比损失要大于在值期权的损失。相应的风险阈值也应该考虑到这个效应。

我们后面将在专门的章节介绍适用于资产管理公司的压力测试方案。