邦贝利：分析术杰出大师的引入与科学家相约

分析术杰出大师邦贝利

虚数的引入是人类在对数的认识过程中向前跨出的一大步，“虚数”这一名词是由笛卡尔在他的《几何》中首先创用的，大数学家欧拉最先引进了虚数符号“i”。在虚数的引入和应用过程中我们还应该提到另一个人的名字，那就是意大利数学家邦贝利。

邦贝利（Bombelli Rafael，1526～1572）1526年出生于意大利波伦亚的一个商人之家。大学毕业后成为一名水利设计工程师。但他酷爱数学，业余时间勤于钻研，著有《代数学》五卷，大约完成于1556年～1560年间。在这部著作中，邦贝利主要系统总结了代数方程理论。他采用了一些较为新颖的符号，并首次提出用连分数逼近平方根的方法。

为了系统总结前人解三次、四次方程所取得的成果，邦贝利从基本定义和符号入手，全面讨论了各种方程的求解方法。他主要研究了5种二次方程、7种三次方程和42种四次方程，针对每一种方程，给出了解法及例题。

卡尔达诺在研究二次方程时就已经遇到过虚数根的问题，但他只把类似于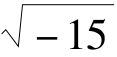“（5+）（5-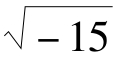=25-（-15）= 40”之类的运算当作算术中“既精妙又无用”的技巧。另外，卡尔达诺也没有解决三次方程判别式为负的情形。在《代数学》中，邦贝利讨论了卡尔达诺没能解决的三次方程不可约情形，即方程的根是实数，而应用求根公式解方程时却出现平方根下为负数的表达式。邦贝利没有像卡尔达诺一样认为虚数是无用的，而是认真地看待了虚数。他证明了卡尔达诺给出的求根公式依然适用于这种情形，给出了相当于我们现在所说的虚数单位“i”的名词：“需要把它加上时，我把它叫做‘负之正’，若要减去它时，我叫它‘负之负’”。基于这样的认识，邦贝利解决了这一类三次方程，指出这一类方程通常有三个实数根，这在复数发展史上是具有里程碑式的重要意义的。

邦贝利还建立了虚数的运算法则。由于当时还没有引进虚数符号“i”，邦贝利的运算法则并不是以现在所见的形式给出的，如他是这样叙述乘法法则的：

正乘以负之正得负之正；……即（+1）（i）=+i；

负乘以负之正得负之负；……即（-1）（i）=-i；(www.xing528.com)

正乘以负之负得负之负；……即（+1）（-i）=-i；

负乘以负之负得负之正；……即（-1）（-i）=+i；

负之正乘以负之正得负；……即（+i）（+i）=-1；

负之正乘以负之负得正；……即（+1）（-i）=+1；

负之负乘以负之负得负；……即（-i）（-i）=-1；

在《代数学》第五卷中，邦贝利还研究了著名的古希腊几何难题三等分角问题。他指出三等分角问题可以转化成解不可约情形的三次方程的问题，从而建立了从理论上证明不能通过尺规作图解决三等分角问题的基础。

邦贝利被誉为意大利文艺复兴时期最后一位代数学家，曾被德国数学家莱布尼兹称为“分析术的杰出大师”，在自己的教学过程中将邦贝利的著作作为学生学习三次方程的基础课本。事实上，《代数学》是文艺复兴时期意大利出版的最有系统的代数著作，加速了方程理论等相关代数知识在西方的传播。