水动力弥散方程在土壤石油类污染物迁移中的应用

6.2.1　水动力弥散方程描述

研究水动力弥散现象以水动力弥散方程为基础。水动力弥散方程又称为对流弥散方程，或弥散对流方程。关于非饱和流中的水动力弥散方程，可根据质量守恒原理直接从饱和流水动力弥散方程得到。方程所涉及的变量和参数在每个空间点处的值都是在表征体元上平均意义上的值［70，149］。因此，可直接导出宏观水平上的水动力弥散方程。设C表示溶质浓度；qx，qy，qz分别为达西定律在x，y，z方向的通量，n为孔隙率。以下根据质量守恒定律和费克定律来推导水动力弥散方程。

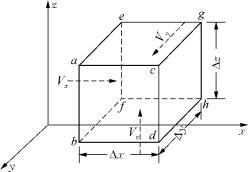
图6－1　单元体

在所考虑的均质各向同性渗流区中任取一单元体，如图6－1所示。在dt时段内，引起单元体中溶质质量变化的主要有对流和弥散两种作用（暂时忽略吸附等因素的影响）。它们引起单元体内溶质质量的变化分别计算如下：

1）对流作用引起溶质质量变化

设M1x，M1y，M1z分别代表在dt时段内x，y，z方向流入单元体的溶质质量增加量，则下式成立。

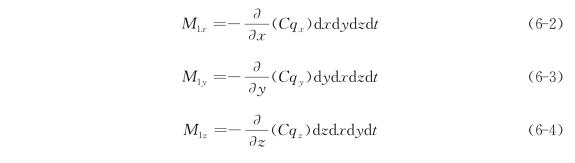
2）弥散作用引起的溶质质量变化

设Jx，Jy，Jz分别代表dt时段内沿x，y，z方向的弥散通量；M2x，M2y，M2z分别代表dt时段内沿x，y，z方向由于水动力弥散而产生的质量增量，它们分别为

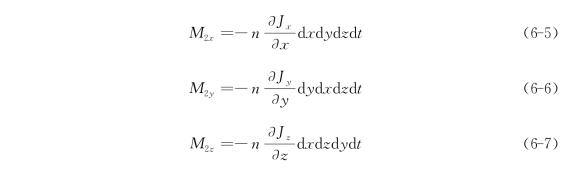
根据质量守恒定律，单元体内由对流和弥散在dt时段内引起的溶质质量变化的代数和，应等于该单元体内溶质质量的变化即有

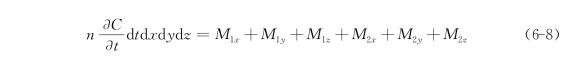
将式（6－2）～式（6－7）带入式（6－8）得：

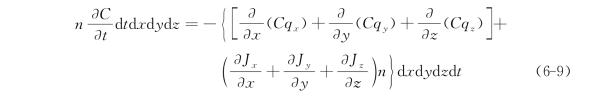
将式（6－9）除以ndxdydzdt得

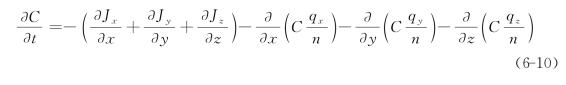
以费克定律和孔隙流速代入

式（6－10）得水动力弥散方程为

（i，j＝1，2，3；x1＝x，x2＝y，x3＝z）（爱因斯坦求和约定），式（6－11）展开为

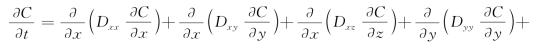
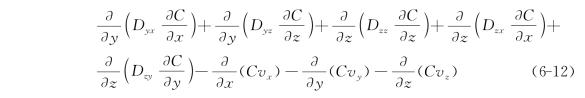
简写为

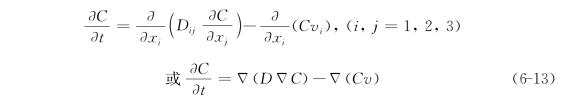
6.2.2　水动力弥散方程的扩充

设F表示固相中的溶质浓度，即单位体积的固相所含的溶质的质量。令f（C，F）表示单位时间单位体积的多孔介质中，由固相进入液相中的溶质质量，对于液相来说，这时的水动力弥散方程为［149，190］

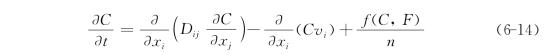
在这种情况下，对于固相单位时间单位体积的溶质质量的减少为

将式（6－15）代入式（6－14）得

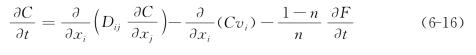
式（6－16）即为吸附解吸情况下的水动力弥散方程。

引进溶液中的溶质浓度C与固相中的溶质浓度F的关系。

非均衡条件下有

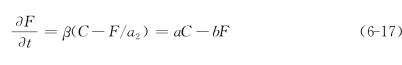(www.xing528.com)

其中，β，a2，a，b均为常数。

均衡条件下有

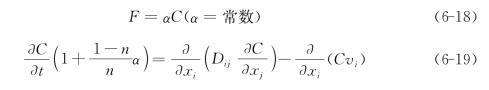
设即得

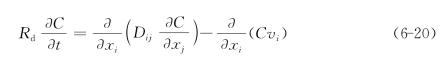
显然Rd＞1，从式中可见，它相当于把弥散系数和孔隙平均流速缩小了，使穿透曲线向后推迟，其效果是减弱了弥散进程，可称Rd为迟滞因子。

令θ表示土壤含水率；I＝aC/at。则衰减时的弥散方程为［189］

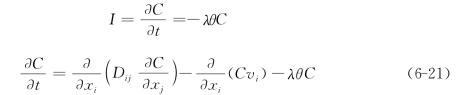
同时考虑吸附、解吸和衰减，达到平衡（F＝αC）时有

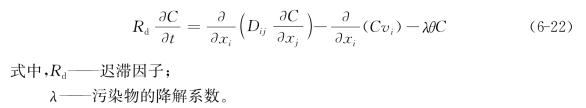
再考虑到单位时间内含水饱和率的变化对水动力弥散过程的影响，变化量为，综合考虑各因素即得如下形式的污染物水动力弥散方程

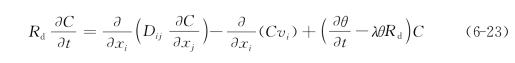
式中出现了混合偏导项，只要坐标轴方向和弥散系数张量的主方向一致就会出现如下简化形式

仿照上述推导方法亦可推导出水运动方程为

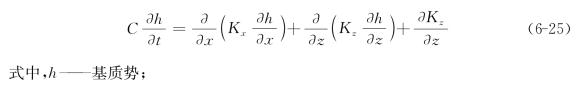
6.2.3　水动力弥散方程的定解条件

污染物迁移方程及其相应的水运移方程，描述了污染物在包气带及地下水中迁移转化的一般规律。为了求解迁移方程，必须确定其相应的初始条件和边界条件。

1）初始条件

在区域Ω上给定初始时刻的浓度分布，其数学表达式为

式中，f（x，y，z）是已知函数。通常都假定研究区域内的浓度是定常数。

2）边界条件

边界条件可分为三种类型［189－191］。

（1）第一类边界条件 给定边界Γ1上的浓度分布，其数学表达式为

式中，C0（x，y，z，t）对给定的边界是时间和空间的函数。

（2）第二类边界条件 给定确定的边界Γ2上的浓度梯度，即给定弥散通量的边界条件，其数学表达为：

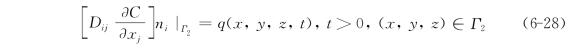
式中，q是已知函数，ni是余弦。对不透水边界，q变为零。

（3）第三类边界条件 给定确定的边界Γ3上的边界浓度分布及梯度，即：给定溶质通量的边界条件，其数学表达式为

式中，g是已知函数；左侧第一项表示弥散通量，第二项表示对流效应。